Problème (fonction trinôme du second degré)

Bonsoir,

nous avons une série de problème à résoudre, et apparemment d'après mon professeur celle-ci est spécialement difficile à résoudre...

Voici l'énoncé :

L'arche d'un point a la forme d'une parabole s'appuyant sur deux points au sol distants de 160mètres. Le sommet de la parabole est à une hauteur de 80 mètres.

Déterminer la hauteur de l'arche à 16 mètres du bord.

Voici mon schéma...:

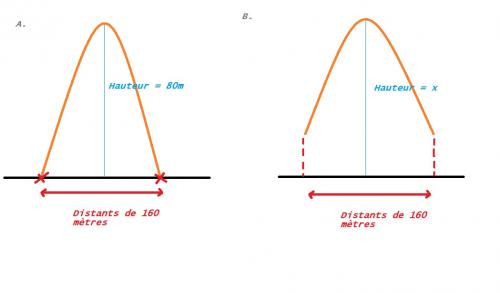
$fichier math$

A. est la parabole initiale.
B. est la parabole éloignée des bords à 16 mètres.

Est-ce bien correct s'il vous plait?

Bonsoir alithekpop

Le schéma B n'est pas correct, A partir des points de contact de l'arche avec l'axe des abscisses, tu places un point à 16 m du bord et tu traces la perpendiculaire à l'axe des abscisses. elle coupe la parabole en un point tu détermines l'ordonnée de ce point. Cette valeur correspond à la hauteur demandée.

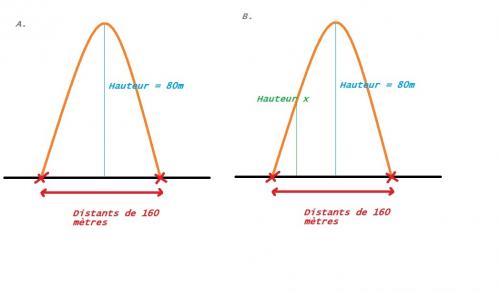
$fichier math$

Voici la modification! Où j'ai oubliée de mettre mais la distance de 16 mètres et d'attribuer un point à l'intersection de cette nouvelle "droite" avec l'axe des abscisses.

Le schéma est correct.
Cherche l'équation de la parabole.

Je n'y arrive pas du tout.

J'essaye au départ de trouver l'équation du schéma A. mais je n'y arrive pas..

Tous ce que je trouve pour l'instant pour le schéma A. c'est un brouillon qui m'a fait :

80 = sommet de la parabole donc 80 = -b/2a

Je remplace x1 et x2 par X1 = a et X2 = b

comme la parabole admet un maximum alors a est négatif

sachant que je remplace -par exemple- x1 par -1 et x=160 car ils sont distants de 160mètres alors ça me fera :

80 = -b/2a
80 = -160/2(-1) = 80

Bon voilà ma méthode étrange qui m'a ramené à ça pour la A...

Attention,

le sommet de la parabole a pour abscisse x = -b/2a
Pour ton tracé, x = 0 et y = 80
donc ....

Ah je me suis trompée dans la formule alors.

Du coup je n'y arrive pas...

le sommet de la parabole a pour abscisse x = -b/2a
Pour ton tracé, x = 0 et y = 80, donc b = 0

y = ax² + 80
si x = 80, y = 0, tu en déduit la valeur de a