géometrie plane et équation

Bonjour,

Me voilà confrontée à un exercice à rendre, cependant je suis handicapée par une simple chose, je n'ai pas compris la question...

Voici mon énoncé :

A et B sont deux points du plan tels que AB = 1. M est un point du segment [AB]. On construit dans le même demi-plan les points P et Q tels que AMP et MBQ sont des triangles équilatéraux.

voici le shéma de la figure :

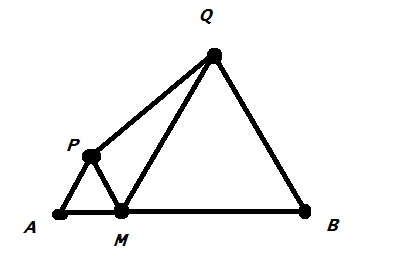
$fichier math$

Je vous remercies d'avance.

Bonjour,
La figure est correcte : P et Q sont du même côté par rapport à la droite (AB).
Mais quelle est cette question que tu ne comprends pas ?

Excusez-moi, j'ai oubliée de marquée ma question :"Démontrer la postition de M qui rend maximale l'aire du triangle MPQ "

Quelle est la mesure de l'angle PMQ ?
Pose x = AM.
Trace la droite passant par P et perpendiculaire à (MQ) : elle coupe (MQ) en H.
Calcule PH et MQ en fonction de x.

Voici pour l'instant ma figure donné :

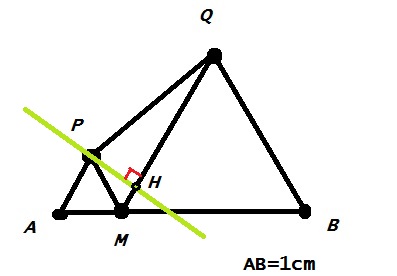
$fichier math$

AB = 1 et AM = x.
Que vaut BM ?

Je vais essayer de continuer, pour moi vous me demandiez de faire ça :

x = AM = PA = PM

PH = PM + MH
PH = x + MH
MQ = AB - AM
MQ=AB-x

Est-ce bien cela que vous m'aviez demandé?

Donc BM = AB-x

Mais AB = 1, donc BM = 1-x.
BMQ est équilatéral, donc que vaut MQ ?

Donc du coup MQ est également égal à 1-x

Citation

PH = PM + MH
PH = x + MHPourquoi un signe moins ?
Attention : il s'agit de distances, pas de vecteurs.
Je résume :
AM = x
BM = 1-x
Le triangle BMQ est équilatéral. Que vaut MQ ?

PS : attend mes réponses sinon les messages se croisent et on ne comprend plus rien.

Et PM ?

C'était pas un signe "-" mais juste un tiret excusez-moi pour la confusion...

Donc je reprends :
AM=x
BM=1-x

Et comme un triangle équilatérale a pour tous ses côtés la même longueurs, alors AM = PM = x

PM = x
ou encore PM = AB-MB

Citation
ou encore PM = AB-MBA éviter car les points ne sont pas alignés.
Quelle est la mesure de l'angle PMQ ?

On nous la donne pas?

Faut il

On ne donne aucune mesure d'angle.
Par contre, on donne des triangles équilatéraux.
Quelle est la mesure de l'angle AMP ? Celle de l'angle BMQ ?
Tu peux en déduire celle de l'angle PMQ.

Ah, oui effectivement !

Donc je récapitule :

AM = x
BM = 1-x
AM = PM donc PM = x

Comme les triangles PMA et MQB sont des triangles équilatéraux, cela me permet d'en déduire que chacun que leurs angles sont égales à 60°.

Je peux en déduire les angles de :

→ AMP : 60°
→ BMQ : 60°

et ainsi de PMQ : 180 - 60 + 60 = 60°

Est-ce bien cela?

Bonsoir alithekpop,

C'est correct;

Calcule la hauteur puis l'aire du triangle.

Le triangle PMQ?

Oui,
pour le triangle PMQ.

Je ne vois pas comment on pourrait faire, à moins que le résultat comprenne pas des chiffres mais des variables...?

oui, il sera en fonction de x.
Exprime PH en fonction de x.

Là, je n'y arrive absolument pas...

Les seules informations dont je dispose sont : PMQ = 60°
...Peut-être y a-t-il un lien avec la relation de Chasles?

Non, la trigonométrie
PH = PM sin 60°
PH = ....

Mon professeur nous a dit d'utiliser la théorème de Pythagore, ce dont je viens de me rendre compte.

cela va nous mener à trouver une équation correspondante à la hauteur de PH en fonction de des informations dont je dispose...

Le théorème de Pythagore est définie par la relation :

PM²=PH²+MH²

Est-ce bien cela?

Non,

Tu pourras utiliser le théorème de Pythagore si tu as démontré que le triangle était rectangle.

La médiane passe par le sommet du triangle PMQ et coupe perpendiculairement le côté opposé à P, en un nouveau point : H. Donc PHM est triangle rectangle.

PH n'est pas une médiane mais la hauteur,
le triangle PMH est rectangle en H car tu as tracé la hauteur.

Puis après avoir démonter cela, il faut faire :

PM²=PH²+MH²
x²=PH²+(1/2x)²
PH²=x²+(1/2x)²

est-ce bien cela?

Une erreur de signe.
PM²=PH²+MH²
x²=PH²+(1/2x)²
PH²=x²-(1/2x)²
= ......

Simplifie puis exprime PH en fonction de x.

PH²=(3/4x)²?

PH²=3/4x²
donc PH = √3/2*x

En traçant la médiane passant par le sommet M coupant le milieu du côté opposé (AP) en N, j'utilise le théorème de pythagore et je tombe sur la même valeur. Donc j'ai MN=√3/2. Je calcul ensuite l'aire du triangle PMQ (L*h/2) cela me fait :

MQPH/2
⇔(1-x)(√3/2)/2
⇔(1-x)*(√3/2)*1/2
⇔(1-x)*√3/4x
⇔√3/4x-√3/4x
soit -√3/4x+√3/4x

est-ce juste?

Indique tes calculs pour MN Quel triangle rectangle utilises tu ?

Pour l'aire du triangle :
MQPH/2
⇔(1-x)(√3x/2)/2
⇔(1-x)*(√3x/2)*1/2
⇔(1-x)*√3x/4
⇔√3/4x-√3/4x²
soit -√3/4x²+√3/4x

J'utilise le triangle PMN :

PM²=MN²+NP²
x²=MN²+(1/2x)²
MN²=x²-(1/2x)²
MN²=(3/4x)²
MN=√3/2x

Il faut justifier qu'il est rectangle.

J'ai tracé la médiane passant par le sommet M coupant le milieu du côté opposé (AP) en N, créant le triangle rectangle PMN.

Comment prouves tu que le triangle PMN est rectangle ?

Citation
J'ai tracé la médiane passant par le sommet M coupant le milieu du côté opposé (AP) en N, créant le triangle rectangle PMN.?

Le tracé de la médiane m'implique pas que le triangle est rectangle.