Suites et raisonnement par récurrence

[mavitr3]

u est la suite définie par $u_1$ = 1/2 et pour tout nombre entier n, $u_{n+1}$ = $1/(2-u_n$)
On se propose de calculer la valeur exacte du produit :
$P_n$ $=$\prod_{k=1}^{n}{}$u_k$ = $u_1$ × ... × $u_n$

Partie 1

1. A l'aide d'un tableur, calculer les premiers termes des suite u et P et tracer les nuages de points associés.
   Expliquer pourquoi les allures obtenues incitent à travailler sur les écritures fractionnaires $u_n$ et $P_n$.
2. Utiliser un logiciel de calcul formel et un algorithme simple pour calculer les termes des suites u et P.
3. Émettre deux conjectures, l'une sur $u_n$, l'autre sur $P_n$, en fonction de n.

Partie 2

1. Démontrer par récurrence l'expression conjecturée pour $u_n$.
   2)a) Exprimer $P_{n+1}$ en fonction de $P_n$ et $u_{n+1}$.
   b) Démontrer par récurrence l’expression conjecturée pour $P_n$.
2. Déterminer les limites des suites u et P.

Voilà j'ai cet exercice à f aire pendant les vacances, ayant subi une opération de l'appendice j'ai raté beaucoup de cours et est fini de rattraper aujourd'hui mais ne comprend pas ce chapitre. Pouvez vous m'aider à résoudre cet exercice. Merci beaucoup pour votre aide précieuse.

[Noemi]

Bonjour mavitr3,

Indique tes éléments de réponse et la question qui te pose problème.
As tu calculé les premiers termes ?

[mavitr3]

Bonjour,
J'ai calculer les termes à l'aide du tableur, j'ai fais les nuages de points mais je ne sais pas si cela est correct.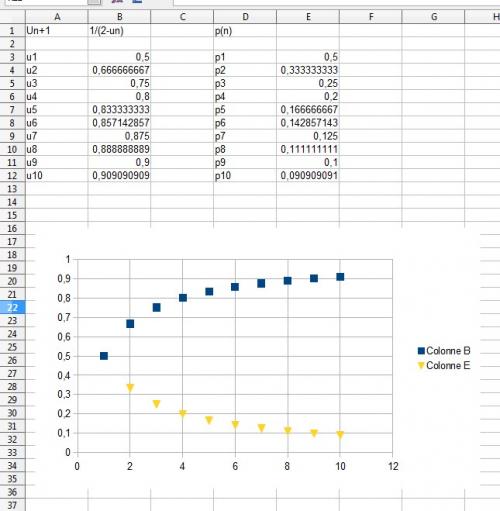

[Noemi]

Bonjour mavitr3,

C'est correct, vers quelle valeur semblent tendre les deux suites ?

[mavitr3]

Les deux suites semblent tendre vers 0 ou 1, non ?

[Noemi]

Oui,
précise celle qui tend vers 1 et celle qui tend vers 0.

[mavitr3]

Donc la suite u tend vers 1 et la suite P tend vers 0

[Noemi]

C'est correct.