Problème de canal.. Minimum d'une fonction

Bonjour !
Je suis face à ce problème et je ne vois pas comment le continuer
Merci

On veut faire circuler un fluide avec un frottement minimal dans un canal à section intérieur rectangulaire dont l'aire est fixée et vaut 2dm². Le canal n'est pas fermé sur le dessus. On admet alors que le frottement est minimal lorsque la somme des longueurs des parois intérieurs(il y en a 3) est minimal

Apporter une réponse au problème en justifiant votre démarche.

Tout d'abord,
J'ai converti en mètre l'aire d'où A= 0.02m²
J'ai appelé l (BC) sur le dessin y (le dessin je l'ai trouvé en ligne car je n'arrivais pas à joindre le mien)
d'où y = 0.02/x

J'ai ensuite calculer le périmètre P (du contour intérieur)= AB + BC+ CD
= x=0.02/x+x
= 2x+0.02/x

Je pensais faire un tableau de variation car dans mon cours on fait cela mais je ne sais pas comment faire sur internet j'ai entendu parler de dérivée mais on a la pas encore vu..
Pourriez-vous m'indiquer comment faire si c'est bien le tableau de variation qu'il faut utiliser ici merci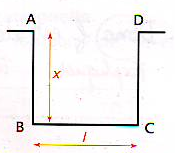

$fichier math$

Bonjour KN,

Réduis l'expression au même dénominateur et cherche le minimum pour le numérateur.

Merci bien
Sous le même dénominateur je trouve alors : 200x²+2/100x

Etudie les variations de cette fonction.

Je trouve donc comme tableau

200x²+2/100x décroissante sur ]-∞; 0[ et croissante sur ]0,+∞[
avec une double barre sous le 0 ?

Mais ensuite comment répondre au problème ? merci

Vérifie tes calculs pour les variations.
Sur ]0 ; +∞[, la fonction est décroissante puis croissante, donc il existe un minimum.

J'explique mes calculs car je ne vois pas comment faire :
Delta = b²-4ac
100^2 -42002
(La première fois j'avais fait 0^2-42002)
=8400
X1≈ -0,48
X2≈ -0,02
D'où -∞; -0,02 décroissante
-0,02; -0,48 décroissante
0 +∞ croissante
Je suis consciente que c'est faux mais je ne vois pas d'où ?
(De plus pour vérifier ma calculatrice me trace une fonction linéaire donc ca n'aide pas vraiment )

Pour l'équation 200x² + 2 = 0
delta = 0²-42200 = -1600
delta négatif donc pas de racine réelle à l'équation

Mais pourquoi chercher les valeurs qui annulent le numérateur ?

Comment détermines tu les variations d'une fonction ?
Calcul du taux de variation ?

Je ne sais pas ne fait on pas comme ça ?
Et aussi pour utiliser la propriété f(x) est du signe de a pour tout x appartenenant a R

Je détermine les variations d'une fonction avec u(x) et Y (lambda) et les différentes propriétés (comme si x associe u(x) et lambda >0 alors x associe u(x) et x associe u(x) + lambda ont le même sens de variation sur I...)

Je ne sais pas ce qu'est le taux de variation ?

Pour x > 0,
La fonction f(x) = 2x est croissante alors que la fonction g(x) = 0,02/x est décroissante donc on ne peut pas conclure sur la fonction f + g

Calcule [f(x2) - f(x1)]/ (x2 -x1)

Je suis vraiment désolée mais je ne comprends pas votre dernier message
Pourquoi parler d'une fonction 2x et reparler de 0,02/x
De plus je ne comprends pas pourquoi faire ce calcul et ce qu'il représente (x2 et X11 ?) ? Je suis désolée de vous déranger

La fonction de départ est 2x + 0,02/x qui est la somme de 2x et 0,02x.

Ensuite j'ai noté le taux de variation [f(x2) -f(x1) ]/(x2 - x1) ou
[f(a+h) - f(a)]/h
as tu dans le cours une de ses formules ?

D'accord alors on a plus besoin de mettre cela sous le même denominateur ?

Non je n'ai pas de formule dans mon cours car comme je le disais on a construit des tableaux de variations qu'avec les fonctions de référence x associe x^2, x associe √x et x associe 1/x

L'année derniere en ses on avait utilisé cette formule
Taux de variation = (valeur d'arrivée -valeur de départ)/ valeur de départ *100
Mais ce ne doit pas être de ca que vous parlez...

Mais je veux bien utiliser cette formule ca pense qu'il n'y a pas d'autre solution seulement que représente X1 et x2 dedans ?

Merci

Sinon j'ai vu sur internet qu'il fallait utiliser la dérivé et j'ai trouvé des formules
A la fin je trouve f'(x) = (2002x+0)/1001
Ce qui me donne 4x ?

Ça ne doit pas être du tout ça... Je ne vois pas comment faire

La dérivée proposée est fausse
f'(x) = 2 - 0,02/x²,

Mais si tu n'as pas vu les dérivées, ni le taux de variation d'une fonction en cours tu ne peux pas utiliser ces éléments.

Utilise le tableau de valeur et/ou la représentation graphique.

D'accord merci oui je pense avoir enfin trouvé ! Merci

Tu as trouvé le minimum ?

X=0,1 ?

Oui
x = 0,1 m , il faut aussi donner la valeur de l.