Représenter graphiquement une fonction avec valeurs absolues
-
PPlop1 dernière édition par Hind
Bonjour, j'ai un exercice de maths que je ne comprends pas que voici :
h:R→R
x→2|x−3| − |x+ 1|+ 2x
Représenter graphiquement Ch et résoudre l’équation h(x) = 1Merci de m'aider.
-
mtschoon dernière édition par

Bonsoir,
Piste,
Suivant les valeurs de x, tu dois trouver le signe de (x-3), celui de (x+1)
Tu as 3 cas à étudier :x ≤ -1 , -1 ≤ x ≤ 3 , x ≥ 3
Dans chaque ces, tu déduis l'expression des valeurs absolues puis l'expression de h(x)
Je te fais le premier cas :x ≤ -1
x-3 < 0 donc |x-3|=-(x-3)=-x+3
x+1 ≤ 0 donc |x+1|=-(x+1)=-x-1h(x)=2(-x+3)-(-x-1)+2x=...=x+7
Tu traîtes avec la même démarche les 2 autres cas.
Tu obtiendras une fonction affine par intervalle.
-
PPlop1 dernière édition par
Bonjour,je ne comprends pas pourquoi je dois étudier x ≤ -1 , -1 ≤ x ≤ 3 , x ≥ 3 et pourquoi dans le premier cas par exemple, vous dites que x-3 < 0 ?
-
mtschoon dernière édition par

Tu as deux expressions avec des valeurs absolues.
Pour |x-3|, l'expression change suivant que x est inférieur ou supérieur à 3
Pour |x+1|, l'expression change suivant que x est inférieur ou supérieur à -1En faisant la synthèse des deux, tu as 3 cas à envisager :
x ≤ -1 , -1 ≤ x ≤ 3 , x ≥ 3
Pour plus de clarté, tu peux disposer ton travail sous forme de tableau:
une ligne pour x ( avec les valeurs -1 et 3)
une ligne pour(x-3) (en mettant le signe dans chaque case)
une ligne pour|x-3| (en mettant l'expression affine dans chaque case)
une ligne pour(x+1) (en mettant le signe dans chaque case)
une ligne pour |x+| (en mettant l'expression affine dans chaque case)
une ligne pour h(x) (en mettant l'expression affine dans chaque case)
-
mtschoon dernière édition par

Citation
pourquoi dans le premier cas par exemple, vous dites que x-3 < 0 ?réponse : si x est inférieur à -1 , à forciori, il est inférieur à 3 donc x-3 < 0
REMARQUE : Si tu as dés diffcultés à comprendre la notion de valeurs absolues, je te mets un lien pour consulter éventuellement
-
PPlop1 dernière édition par
Ok merci, donc pour le troisième cas x ≥ 3
x-3 > 0 donc |x-3| = x-3
x+1> 0 donc |x+1|= x+1h(x)=2(x-3)-(x+1)+2x=...
Le bon résonnement ?
-
mtschoon dernière édition par

Pour x ≥ 3 , ton raisonnement est bon et tu dois trouver 3x-7
Il te reste à faire le cas -1 ≤ x ≤ 3
-
PPlop1 dernière édition par
-1 ≤ x ≤ 3 comment je peux faire cela ?
-
mtschoon dernière édition par

Comme pour les deux autres cas.
Pour -1 ≤ x ≤ 3
x-3 ≤ 0 donc |x-3|=...
x+1 ≥ 0 donc |x+1|=...Pour que tu puisses vérifier tes calculs, je te donne l'expression que tu dois trouver pour h(x) dans ce cas : h(x)=-x+5
-
PPlop1 dernière édition par
Oui j'ai vérifié. Maintenant que j'ai exprimer H(x) dans les 3 cas que faire ?
-
mtschoon dernière édition par

Suis l'ordre des questions posées.
Tu dois représenter la fonction h (composée de 3 fonctions affines) :
une demi-droite, pour x ≤ -1, d'équation y=x+7
un segment, pour -1 ≤ x ≤ 3, d'équation y=-x+5
une demi-droite, pour x ≥ 3, d'équation y=3x-7Au final, tu doit obtenir une ligne brisée (continue) en 3 parties.
-
PPlop1 dernière édition par
Comment faire pour trouver des points pour ainsi créer la fonction ?
-
mtschoon dernière édition par

Dur, dur...
Tu ne sais pas tracer des droites ? !
Pour une droite, deux points suffisent .
Pour x ≤ -1 , tu peux prendre par exemple x=-3 et x=-1
Pour -1 ≤ x ≤ 3 , tu peux prendre par exemple x=-1 et x=3
Pour x ≥ 3, tu peux prendre par exemple x=3 et x=5
-
PPlop1 dernière édition par
Merci, reste l’équation h(x) = 1, je dois trouver x pour chaque équation (ex : 1 = x+7) ?
-
Bonsoir Plop1,
Oui tu résous l'équation dans chaque cas et tu vérifies que la valeur de x trouvée appartient au domaine correspondant à l'équation.
-
PPlop1 dernière édition par
1 = x+7 x = -6
1=3x-7 x=-2
1=-x+5 x=-4 ?
-
mtschoon dernière édition par

Ton premier calcul est exact mais il faut t'assurer que -6satisfait à la conditionx ≤ -1.
Comme c'est bien le cas ,-6 convient.Refais tes deux derniers calculs (puis vérifie si les valeurs trouvées conviennent ou non).
-
PPlop1 dernière édition par
-2 convient cependant -4 ne fonctionne pas.
-
mtschoon dernière édition par

je t'ai dit derefaire tes deux derniers calculscar ils sont faux.
Recompte les.
3x-7=1 <=> 3x=1+7 <=> x=..........
-x+5=1 <=> -x=1-5 <=> -x=-4 <=> x=...............
-
PPlop1 dernière édition par
x = 8/3 qui correspond
x = 4 qui correspond.
-
mtschoon dernière édition par

Cette fois tes calculs sont exacts mais les valeurs trouvées se sont pas satisfaisantes...
8/3 doit satisfaire à la condition x ≥ 3 . Réponse ?..............
4 doit satisfaire à la condition -1 ≤ x ≤ 3 . Réponse ?..............
-
PPlop1 dernière édition par
Non et non.
-
mtschoon dernière édition par

exact.
La seule solution à l'équation h(x)=1 est donc -6
Tu as résolu cette équation algébriquement.
J'ignore si l'interprétation graphique est demandée, mais vu que tu as représenté la fonction h, pour que ce graphique serve, tu peux représenter (sur le même graphique) la droite (horizontale) d'équation y=1
Tu pourras ainsi vérifier la réponse trouvée à l'équation
Voilà ce que tu dois obtenir
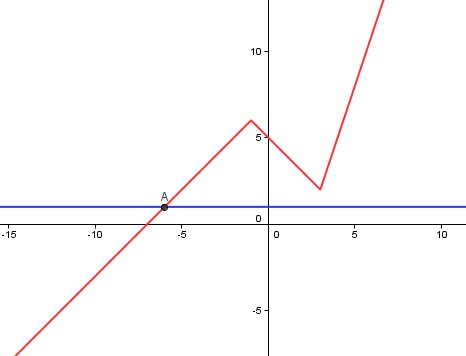
-
PPlop1 dernière édition par
Merci.
-
mtschoon dernière édition par

De rien !
A+