tracé de droites Algorithme avec Algobox
-
MMiiche36 dernière édition par
Bonjour voilà je dois faire un algorithme sur algobox qui permet de tracer les droites d'équation respectives ax + by + c = 0 et a'x+b'y+c'= 0 et de déterminer si elles sont secante par conséquent il donne les coordonnées du point d'intersection sinon il détermine si elles sont parallèles ou confondus.
Je sais pas trop comment mis prendre pour réalisé cette algorithme et j'aimerais bien avoir de l'aide svp merci d'avance.
-
Bonjour Miiche36,
Comment prouve t-on que deux droites sont parallèles ?
sécantes ?
Comment détermine t-on les coordonnées du point d'intersection ?
-
MMiiche36 dernière édition par
SI (axb' -a'xb=0 ) les deux droites sont parallèles
sinon
les droites sont sécantes pour trouver le point d'intersection il faut résoudre l'équation à deux inconnu
ax+ by=c
a'x+ b'y=c'
SI (axb' -a'xb=0 ) et (cxb'-c'xb=0)les droites sont confondus. C'est correct?
-
C'est correct,
tu peux débuter l'algorithme.
-
MMiiche36 dernière édition par
Merci! sauriez vous comment faire pour tracer les droites sur algobox? Svp
-
mtschoon dernière édition par

Bonjour,
Je vois que tu n'as pas eu encore de réponse à ta dernière question.
Je t'indique le principe relatif au tracé de segments sur Algobox.
(tu l'adaptes à ton programme)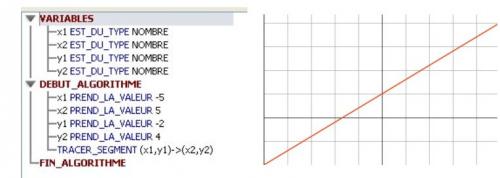
Pour obtenir l'instruction "TRACER_SEGMENT" , tu cliques sur l'onglet Dessiner dans un repère que tu vois en bas de l'écran.
Tu cochesutiliser un repère.
Tu peux garder les valeurs par défaut du repère ou tu les changes ( xmin, xmax,...)
Tu cliques sur TRACER SEGMENT (et tu renseignes les cases de coordonnées)
-
MMiiche36 dernière édition par
Merci beaucoup pour l'aide apportée
-
MMiiche36 dernière édition par
Desolé de vous déranger encore mais je sais pas quoi mettre pour le point de départ x et y pour tracer mes deux droites
-
mtschoon dernière édition par

Pour tracer une droite d'équation ax+by+c=0, avecb≠0,
y=−abx−cby=\frac{-a}{b}x-\frac{c}{b}y=b−ax−bc
Les deux points choisis doivent être sur cette droite.
Je t'indique le méthode pour ce cas (qui est le plus usuel b≠0)
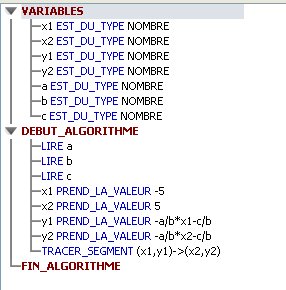
Remarque : pour x1 et x2, j'ai pris -5 et 5 car j'ai réglé xmin et xmax à -5 et 5.
Si tu laisses xmin et xmax à -10 et 10, prends x1 et x2 à -10 et 10
Il est souhaitable que le segment remplisse tout le cadre du graphique, pour mieux illustrer une droite.J'gnore l'énoncé exact de ton devoir, mais si tu dois faire un travail soigné , il faut que tu envisages aussi le cas exceptionnelb=0, où la droite est parallèle à l'axe des ordonnées.
-
MMiiche36 dernière édition par
Bonjour, Merci, je vais essayer de faire sachant que je dois utiliser la boucle tant que. Merci.
-
mtschoon dernière édition par

De rien et bon algorithme.