Fonctions convexes, dérivée seconde et fonctions concaves

Bonjour à tous ! Tout d'abord bonne année à tout le monde, et qui dit bonne année dit forcément un petit devoir maison !

Je tiens à préciser que je n'ai jamais vu la notion de fonction convexe en cours (mais c'est normal vu que c'est un DM) mais que je me suis un peu renseigné avant, cependant j'avoue ne pas avoir compris le but et le fonctionnement de cette "dérivée seconde" (à vrai dire c'est assez flou je n'arrive pas à m'imaginer une fonction deux fois dérivable :().

Le système de la fonction concave étant vraisemblablement lié à la fonction convexe (d'après ce que j'ai compris), je cherche donc ici une âme charitable pour m'aider à comprendre avec des exemples de préférence
Par exemple je peux poster les deux premières questions de mon devoir si cela peut aider
Elles sont les suivantes :

Démontrer que la fonction f est convexe sur I si, et seulement si, la fonction f' est croissante sur I.
Soit f une fonction convexe et soit a ∈ I. Posons, pour tout réel x de I:
ρ $_a$ (x)= f(x)-[f'(a)(x-a)+f(a)]
a) Quelle interprétation graphique peut-on faire de la fonction ρ $_a$ ?

Merci d'avance pour votre aide !

Bonjour,

Les données de ton exercice sont insuffisantes.

Si tu as consulté quelques sites sur le web, tu as pu remarquer des définitions différentes, plus ou moins générales, qui rendent parfois la démonstration de la question 1) très difficile pour le niveau 1S.

Si tu as besoin de conseils, il faut que tu donnes, non seulement les questions, maistoute la partie de l'énoncé qui précède les questions, pour savoir comment interpréter cet exercice.

L'exercice commence par une définition de la dérivée seconde qui est la suivante:

La dérivée seconde de f, notée f'', est la dérivée de la fonction f' ; autrement dit f''=(f')'.
Une fonction f deux fois dérivable sur un intervalle I est dite convexe si sa dérivée seconde est positive sur I.

Ce qui nous amène directement à la question 1 postée précédemment.

Je pense que pour la question 1 il faut travailler avec un cas général (comme pour trouver une propriété), cependant je trouve la question assez difficile effectivement.

C'est ce que j'imaginais.
Tu dois travailler seulement dans le cas d'une fonction deux fois dérivable.
(cas tout à fait accessible en 1S).

Applique tout simplement la définition donnée dans l'énoncé .

Une fonction f deux fois dérivable sur un intervalle I est dite convexe si sa dérivée seconde est positive sur I.

Un exemple simple pour comprendre la dérivée seconde : tu dérives la dérivée première f '

f(x)=x² donc f'(x)=2x donc f"(x)=2

Pour la 1) , utilise la définition donnée

f convexe sur I <=> f"(x) ≥ 0 <=> f' croissante

explication : f' est croissante si et seulement si sa dérivée est positive, c'est à dire f"(x) prend des valeurs positives.

Piste pour la 2)a)

y=f'(a)(x-a)+f(a) est l'équation de la tangente (Ta) au point d'abscisse a de la courbe

Soit M(x,f(x)) un point de la courbe, avec x ∈ I

$strong>p_a$ représente la différence entre l'ordonnée $y_M$ du point M de la courbe avec l'ordonnée $y_N$ du point N de même abscisse x de (Ta)

$strong>p_a$ (x) = $y$ _M $y_N$

$p_a$ (x) > 0 <=> yM > yN <=> M est au - dessus de (Ta)

$p_a$ (x)= 0<=>yM= yN <=> M ∈ (Ta)

$p_a$ (x) < 0 <=> yM < yN <=> M est en - dessous de (Ta)

Merci pour la question 1 j'ai compris Par contre pour la question 2 alors là c'est le flou complet x) Je ne suis pas une bête en maths mais j'avoue ne pas avoir compris ton raisonnement (je n'ai peut-être pas encore vu ça en cours). Je n'ai pas compris pourquoi faire la difference entre Ym et Yn, qu'est-ce qu'ils représentent, ou encore où est passée la fonction ρ $_a$
C'est comme si je ne voyais même pas un rapport avec l'énoncé xD

Désolé d'être aussi nul Tu pourrais m'expliquer avec plus de precisions en utilisant l'énoncé et en prenant en compte que j'suis pas très bon en maths stp, je te serais énormément reconnaissant, merci d'avance

Pour la 2)a), je vais essayer de t'expliquer avec un graphique.

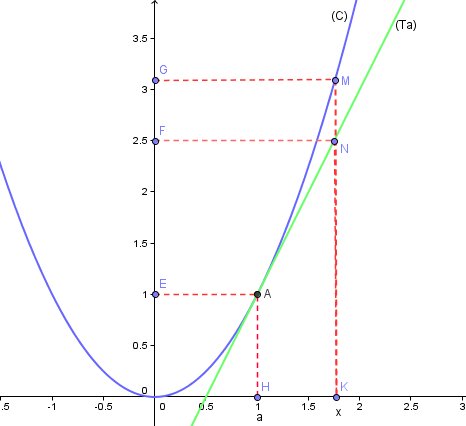
$fichier math$

(C) est la courbe d'équation y=f(x) (en bleu)

(Ta) est la tangente en A à la courbe (en vert)

y=f'(a)(x-a)+f(a) est l'équation de (Ta) ( tu as dû le voir en cours)

Soit x une valeur de I.

M est le point de (C) d'abscisse x
Son ordonnée que j'ai appelée $y_M$ est la mesure algébrique entre O et G (c'est à dire entre K et M)
on a donc** $y_M$ =f(x)**

N est le point de (Ta) d'abscisse x
Son ordonnée que j'ai appelée $y_N$ est la mesure algébrique entre O et F (c'est à dire entre K et N)
on a donc** $y_N$ =f'(a)(x-a)+f(a)**

L'énoncé te dit que** $p_a$ (x)=f(x)-[f'(a)(x-a)+f(a)]**

Donc$\fbox{\text{p_a(x)=y_m-y_n}$

Regarde bien le graphique.

$p_a$ (x) est la différence entre l'ordonnée de M et celle de N

$p_a$ (x) est donc la mesure algébrique entre N et M ( c'est à dire entre F et G)

Si tu connais la notation de mesure algébrique, tu peut écrire :
$\fbox{\text{p_a(x)=\overline{km}-\overline{kn}=\overline{nm}$

C'est ce qui faut que tu expliques dans la question 2)a)

Dans ma réponse précédente, j'ai complété en expliquant à quoi va servir le signe de $p_a$ (x).
Ce n'est pas obligé de l'expliquer là, je suppose que ça sera vu dans les questions suivantes (que tu n'as pas données)

Effectivement dans les questions suivantes il y a une étude de signe !
Merci beaucoup mtschoon pour le temps que tu as consacré à m'expliquer, grâce à toi j'ai compris la notion (même si je trouve bizarre que le professeur nous ai donné ce DM etant donné qu'on a jamais vu en cours que y=f'(a)(x-a)+f(a) m'enfin je suppose qu'il fallait le trouver tout seul ^^') Enfin merci encore et bonne continuation à toi ;D

C'est bizarre que tu ne connaisses pas l'équation de la tangente à une courbe en un point donné.

Si besoin, je te mets un lien où il y a l'explication.

http://homeomath.imingo.net/deritan.htm

Bon travail.