Comment déterminer le signe de la dérivée et le sens de variation de la fonction
-
Aallthekpop dernière édition par Hind
Bonjour, il y a quelque chose que je ne comprends pas :
la fonction :
f(x) = -2x³-2x²+x-5
nous obtenons
f'(x) = -6x²-4x+1
ainsi que le tableau de variations suivant :
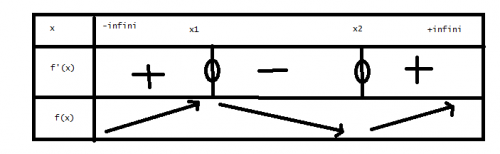
avec x1 = (-1/3)-(√10/6) et x2 = (-1/3)+(√10/6)
CEPENDANT
dans sur cette fonction, tout est différent :
h(x) = -x³+3x²+1
h'(x) = -3x²+6xavec x1 = 0 et x2 = 2
avec son tableau de variations
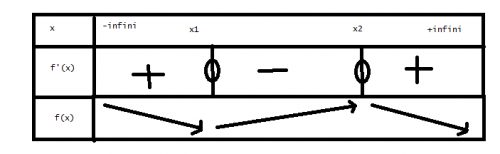
En gros, ma question est : comment peut-on déterminer le signe de la dérivée et le sens de variation de la fonction ?
merci de bien vouloir m'aider!
-
Bonjour alithekpop,
Les deux tableaux de variations sont faux.
Calcule les valeurs qui annulent la dérivée puis fais un tableau de signes pour la dérivée
h'(x) = 3x(-x+2)
x -∞ 0 2 +∞
3x - 0 + +
(-x+2) ...
h'(x) ....
-
Aallthekpop dernière édition par
Ah bon? Mais ce sont pourtant les tableaux de variations du corrigée de ces exercices...
(-x+2) + - 0 +
h'(x) - 0 - 0 +?
-
Ou as tu trouvé ces corrigés ?
x -∞ 0 2 +∞
3x - 0 + +
(-x+2) + + 0 -
h'(x) - 0 + 0 -
donc pour h(x)
décroissante (flèche vers le bas) puis croissante (flèche vers le haut) puis décroissante.Si la dérivée est négative la fonction est décroissante,
Si la dérivée est positive la fonction est croissante.Fais les calculs pour la fonction f.
-
Aallthekpop dernière édition par
Dans le site de corrigée officiel du livre de math que nous utilisons cette année, ce livre ne comporte -normalement- aucunes fautes- et jusqu'ici, tout ce que nous corrigeons en classe correspond aux réponses du corrigé de ce livre...
Mais je crois aux fautes de frappe, car dans ma leçon il est marqué nulle part que quand la dérivée est positive, les variations sont décroissantes, donc vous deviez avoir raison.Oui, excusez-moi je viens de relire mon commentaire, et j'ai fait une erreur que j'ai comprise, mais en conclusion je comprends enfin ce tableau de variation !
-
Que trouves tu pour la fonction f ?
-
Aallthekpop dernière édition par
Pour ce deuxième tableau de variation, je trouve le même que celui que je viens de vous montrer !
-
La fonction f a le même tableau de variation que la fonction h.
seules les valeurs x1 et x2 changent.
-
Aallthekpop dernière édition par
Ah oui effectivement :
x1 = −racinede10−26\frac{-racinede10-2}{6}6−racinede10−2
x2 =−racinede10+26\frac{-racinede10+2}{6}6−racinede10+2est-ce bien cela?
-
Vérifie les signes.
-
Aallthekpop dernière édition par
Pardonnez-moi à la deuxième, cela devient : racinede10-2/6
-
C'est correct.