Dérivations (problème d'optimisation)
-
Aallthekpop dernière édition par
Bonjour, nous avons récemment corrigé ce problème en classe, en voici l'énoncé ainsi que la correction :
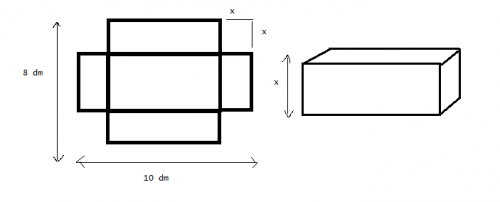
*Avec une plaque de carton rectangulaire de 8 dm par 10 dm, en découpant quatre carrés identiques on obtient le patron d'une boite (sans couvercle !).
*On veut trouver la dimension des carrés à découper pour obtenir une boite dont le volume sera maximum.
Voici la correction :
Longueur du rectangle de base : 10-2x
Largeur du rectangle de base : 8-2x
Hauteur du pavé droit : xDonc le volume de la base en fonction de x est :
V(x) = (10-2x)(8-2x)x
V(x) = 4x³-36x²+80xNous allons étudier les variations de la fonction V x → 12x²-72x+80 sur ℜ.
La fonction V définie sur ℜ par V(x) = 4x³-36x²+80x est une fonction polynôme, donc dérivable sur ℜ avec : pour tout x ∈ ℜ : V'(x) = 12x²-72x+80
Cherchont les valeurs qui annulent V' et étudions le signe de V' sur ℜ. On calcul le discriminant du trinôme : Delta = b²-4ac = (-72)²-(4)(12)(80)=1344
Comme Delta > 0, il existe deux solutions :
x1 = 4,53 et x2 =1,47
On dresse le tableau suivant :
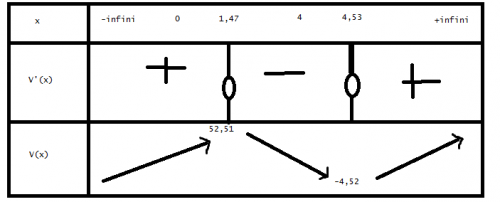
x ∈ ]0;4[ si on se restreint à l'intervalle ]0;4[, alors la valeur max est atteint pour x = 3 - (racine de 2 / 3) ≈ 1,67.
**Voici mes questions :****1/ Pourquoi : x = 3 - (racine de 2 / 3) ≈ 1,67 ? D'où ça vient ?
2/ Pourquoi les variations commencent par être croissante alors que a > 0 ?
3/ Comment a-t-on fait pour trouver 0 et 4 ? (faut-il calculer le discriminant de la fonction V(x) ?)
Merci de m'éclairer...
-
Bonjour allthekpop,
1/ x = 3 - √2/3 est une solution de l'équation V'(x) = 0.
2/ L'équation V'(x) = 0 admet deux solutions comme a = 4 > 0
les signes sont + - + donc la fonction est croissante au début.
3/ la largeur est de 8, donc la valeur maximale de x est 8/2 = 4
de plus x est une dimension soit x≥0 donc on étudie sur [0,4].
-
Aallthekpop dernière édition par
1/ Comment l'a-t-on résolue ? N'a-t-on pas résolue cette équation grâce au discriminant ?
2/ et 3/ Je viens de saisir, merci !
-
Oui pour la question 1, on peut résoudre l'équation en utilisant la méthode avec le discriminant.
-
Aallthekpop dernière édition par
1/ Pouvez-vous me montrer cela s'il vous plait ? Je n'arrive pas à retrouver ce résultat...
-
12x²-72x+80 = 0
tu peux diviser par 4 soit
3x² - 18x + 20 = 0
calcul de delta 84 soit (2√21)²
solution
x1 = (18+2√21)/6 = 3 + √21/3
x2 = 3 - √21/3= 1,47
-
Aallthekpop dernière édition par
Ok ! Cela veut donc dire que je me suis trompée à l'écriture de fin ? Ce n'est pas 1.67 mais 1.47 ?