DM Produit scalaire

Bonjour j'aurais vraiment besoin d'aide rapidement pour ce dm et ce serait vraiment génial si vous pouviez me donnez des explications aussi !

$fichier math$
Voici l'énoncé :
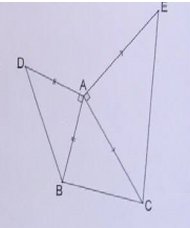
ABC est un triangle quelconque
On construit comme sur la figure ci-contre extérieurement au triangle ABC
les deux triangles ABD et ACE rectangles isocèles en A

Démontrez que AD.AE=-AB.AC
2)En déduide que les droite (BE) et (CD) sont perpendiculaire
Je vous remercie d'avance !!!!

Bonjour,

Ici, les énoncés doivent être écrits à la main.
Seuls les scans de graphiques sans texte sont autorisés.

En plus, il ne faut mettre qu'un seul exercice par discussion.

Merci d'écrire l'énoncé.

Piste pour démarrer,

$ab⃗.ac⃗=ab×ac×cos(ab⃗,ac⃗)\vec{ab}.\vec{ac}=ab \times ac \times cos(\vec{ab},\vec{ac})$

$ad⃗.ae⃗=ad×ae×cos(ad⃗,ae⃗)\vec{ad}.\vec{ae}=ad \times ae \times cos(\vec{ad},\vec{ae})$

$ad⃗.ae⃗=ab×ac×cos(ad⃗,ae⃗)\vec{ad}.\vec{ae}=ab \times ac \times cos(\vec{ad},\vec{ae})$

Il te reste à comparer les angles $(ad⃗,ae⃗)(\vec{ad},\vec{ae})$ et $(ab⃗,ac⃗)(\vec{ab},\vec{ac})$

Avec la relation de Chasles relatives aux angles orientés de vecteurs,

$(2π)(\vec{ad},\vec{ae})=\frac{\pi}{2}+(\vec{ab},\vec{ac})+\frac{\pi}{2}=(\vec{ab},\vec{ac})+\pi\ \ (2\pi)$

Donc les cosinus sont opposés, donc les produits scalaires sont opposés, d'où la réponse.

Je n'ai pas compris... désolé. Serait ce possible de me réexpliquer svp ?

T'expliquer...indique ce que tu ne comprends pas.

Au niveau des propriétés , si vous pouviez indiquez celles que vous utilisez svp !

Pour les produits scalaires :

$u⃗.v⃗=∣∣u⃗∣∣×∣∣v⃗∣∣×cos(u⃗,v⃗)\vec{u}.\vec{v}=||\vec{u}|| \times ||\vec{v}|| \times cos(\vec{u},\vec{v})$

Pour la décomposition des angles :

$(ad⃗,ab⃗)+(ab⃗,ac⃗)+(ac⃗,ae⃗)=(ad⃗,ae⃗)(\vec{ad},\vec{ab})+(\vec{ab},\vec{ac})+(\vec{ac},\vec{ae})=(\vec{ad},\vec{ae})$

J'espère que maintenant, tu as compris la 1)

Pour la 2), je te suggère d'utiliser la relation de Chasles relative aux vecteurs.

$be⃗.cd⃗=(ba⃗+ae⃗).(ca⃗+ad⃗)\vec{be}.\vec{cd}=(\vec{ba}+\vec{ae}).(\vec{ca}+\vec{ad})$

Tu développes : tu obtiens 4 produits scalaires.
Deux sont nuls (car vecteurs orthogonaux) et les deux autres sont opposés grâce à la question 1)

Donc :

$be⃗.cd⃗=0\vec{be}.\vec{cd}=0$

Donc vecteurs orthogonaux, donc droites perpendiculaires.

Bon travail et bonne nuit.

Merci beaucoup !

De rien !