démonstration trigonométrique 2 nde C
-
Ffreemenbf dernière édition par
Bonsoir, je viens par la présente, solliciter votre aide pour la résolution de cet exercice.Bonne reception, merci d'avance.
Soit ABC un triangle isocèle de sommet A tel que BC= a et (vec{BA} , vec{BC})=2π/5. La bissectrice de hat{ABC coupe le côté du segment AC en D. Faire une figure
1- Démontrer que AD=BD=a
2- Démontrer que AB= 2a cos π/5 et CD= 2a cos 2π/5
en déduire que cos π/5 - cos 2π/5=1/2
3- On appel H le projeté orthogonal de A sur le segment BC. Calculer BH en fonction de a de deux manières différentes et en déduire que cos π/5 * cos 2π/5= 1/4
4- En remarquant que (x+y)²=(x-y)²+4xy et des réponses précédentes, déduire le système suivant:cos π/5+ cos 2π/5= (√5)/2
cos π/5- cos 2π/5= 1/2et calculer cos π/5 et cos 2π/5
5- calculer sin π/5 et sin 2π/5
-
Bonsoir freemenbf,
Indique tes calculs et la question qui te pose problème.
As tu fait la figure ?
-
Ffreemenbf dernière édition par
Ré bonsoir, merci de m'avoir répondu.
En faites, j'ai pu faire la figure. C'est la résolution des questions posées que je n'arrive pas.merci d'avance de m'aider
-
Ffreemenbf dernière édition par
Re, Bonjour,
J'avais commencé en disant que:Si la bissectrice de l'angle ABC coupe le côté du segment AC en D cela signifie que la bissectrice divise l'angle 2pi/5 en pi/5. cos pi/5= BD/AR ce qui signifie que AB=BD/cos pi/5.je me suis arrêté là, je n'arrive pas à démontrer, ainsi que les autres questions. Merci de m'aider
-
Oui
l'angle CBD = π/5,- calcule la mesure de l'angle CDB, puis tu conclus sur la nature du triangle BCD.
- Trace AH la hauteur issue du point A, puis exprime HB en fonction de AB.
même raisonnement dans le triangle BCD.
-
Manou Vino dernière édition par
@Noemi j’ai pas trouvé la figure
-
@Manou-Vino Bonjour, (Marque de politesse à ne pas oublier !!)
La figure :
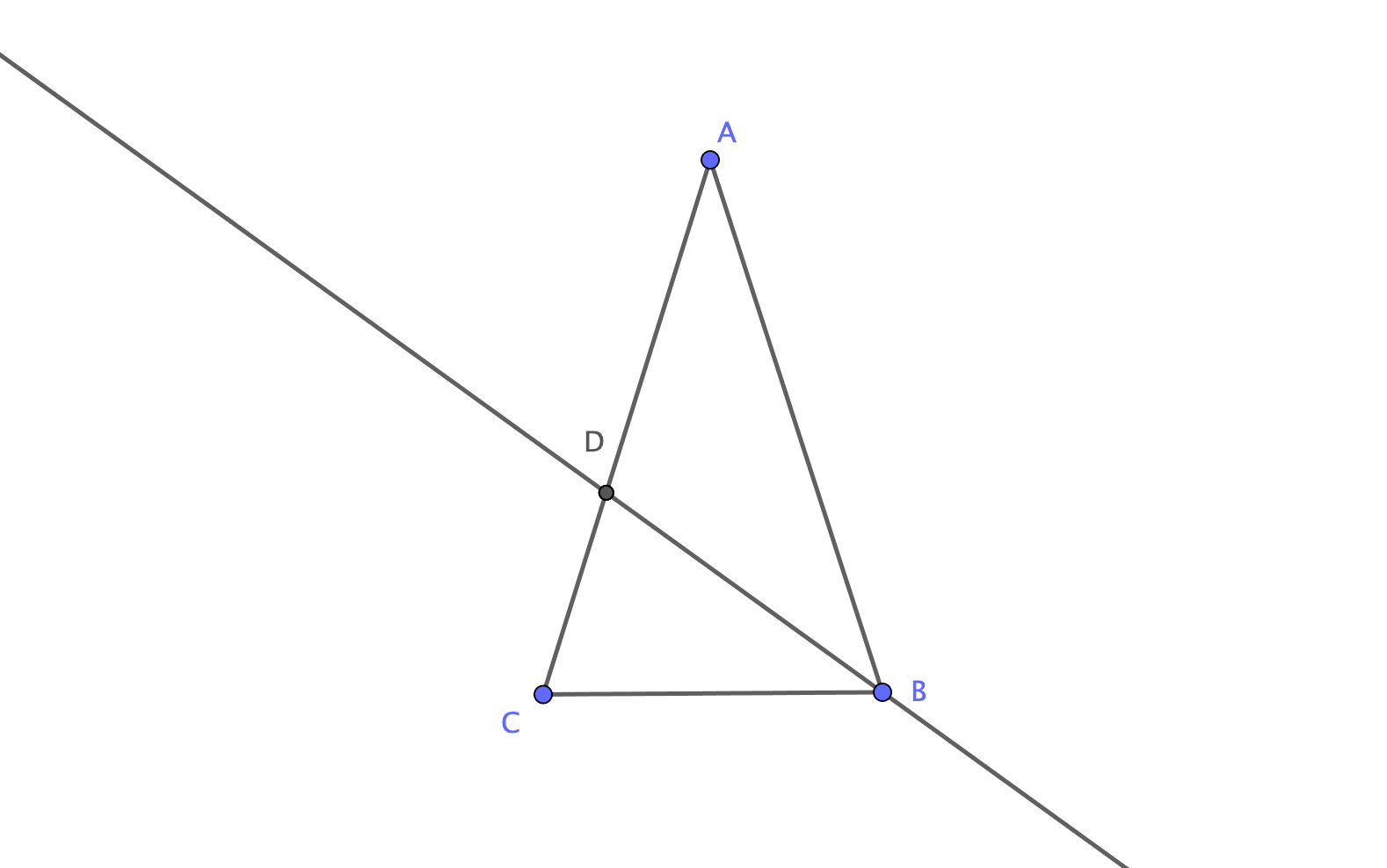
-
Manou Vino dernière édition par
@Noemi merci