Fonction polynome du 2nd degré et algorithme
-
Eelevedeseconde dernière édition par
Bonsoir j'ai un autre problème et je bloque sur une question, merci :
On considère l'algorithme ci-dessous.
Variables: x,y,M sont des nombres réels
Entrée: Saisir M
Traitement: Affecter à x la valeur 0
Affecter à y la valeur 7
Tant que y<M
Affecter à x la valeur x+1
Affecter à y la valeur f(x)
Fin Tant queSortie: Afficher x
- On saisit M = 500 et on exécute l'algorithme pas à pas.
Reproduire et compléter le tableau suivant.
x 0 1 2 3 4 5 6 7 8 9 10 11
y 7 22 43 70 103 142 187 238 295 358 427 502- Quelle est la valeur affichée en sortie ?
La valeur affichée en sortie est 11
- Expliquer le rôle de cet algorithme.
C'est ici que je ne comprends pas trop la question posée.
L'algorithme permet de déterminer quel est le plus petit entier naturel x tel que f(x) > 500, est-ce cela ?
-
Bonsoir elevedeseconde,
L'ensemble est correct.
Quelle est l'expression de f(x) ?
-
Eelevedeseconde dernière édition par
Dans ce même exercice il est marqué juste après, avec g(x)=-3x²+7x+12 faîtes la même chose mais ce n'est pas possible car même en utilisant ma calculatrice ou trouve toujours -31 comment cela se fait-il, merci
-
Eelevedeseconde dernière édition par
Noemi
Bonsoir elevedeseconde,L'ensemble est correct.
Quelle est l'expression de f(x) ?
f(x)=3x²+12x+7
-
Eelevedeseconde dernière édition par
Est ce parceque la parabole est inversé? http://hpics.li/58a1a8b
-
mtschoon dernière édition par

Rebonjour,
Je pense que tu aurais dû rester sur ton topic précédent auquel j'ai répondu,car visiblement, l'expression de f(x) est la même, et tu as déjà étudié les variations de cette fonction.
Effectivement, pour ce qui est de g(x), tu devrais étudier les variations de g comme tu l'as fait pour f (et faire le tableau de variation)
Ici, a=-3 donc a < 0, donc concavité tournée vers le bas.Le sommet a une ordonnée voisine de 16.
Pour tout x, f(x) < 500
M=500
La condition "Tant que y<M" est toujours réalisée.
On ne sort jamais de cette boucle : c'est une**"boucle sans fin"**Le programme tourne indéfiniment.
Matériellement, ta calculette ne peut pas tourner indéfiniment...quand sa capacité de calcul est dépassée, elle envoie un message d'erreur ou elle se bloque .
C'est peut-être ça le "-31" dont tu parles.
-
Eelevedeseconde dernière édition par
Merci, je comprends mieux.
-
mtschoon dernière édition par

De rien (et j'espère que tu comprends tout à fait, sinon reposte).
-
mtschoon dernière édition par

Je viens de taper l'algorithme sur Algobox (pour la fonction g)
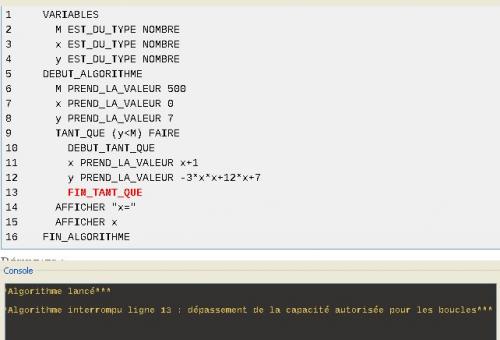
En lançant l'algorithme, regarde le message obtenu (sur fond noir) :
"Algorithme interrompu ligne 13 : dépassement de la capacité autorisée pour les boucles"