Déterminer la position de M pour que l'aire du quadrilatère soit minimale
-
GGabie971 dernière édition par Hind
Bonjour et merci à ceux qui m'aideront pour ce DM:
ABCD est un rectangle de largeur 5cm et de longueur 10cm
Les points M,N,P et Q appartiennent respectivement aux côtés [AB], [BC], [DC] et [AD] tels que AM=BN=CP=DQ
Déterminer, en justifiant, la position du point M pour que l'aire du quadrilatère MNPQ soit minimale
J'ai trouvé que la surface du quarilatère MNPQ = 50-x(10-x)-x(5-x)
= 2x^2-15x+50
Es-ce correcte ?
Et es-ce que pour trouvé la position de M je dois résoudre l'équation 2x^2-15x+50 =0 ?
-
mtschoon dernière édition par

Bonjour,
Pour AM=x avec 0 ≤ x ≤ 5, l'expression de l'aire MNPQ est bonne.
Pour trouver le minimum, tu poses f(x)=2x²-15x+50
Tu étudies les variations de la fonction f sur [0,5]
-
GGabie971 dernière édition par
Mais comment faire ?

-
mtschoon dernière édition par

Peut-être connais-tu les fonctions polynômes du second degré ?
Regarde ton cours ou celui de l'an passé.f(x)=ax²+bx+c
Pour a >0, f a son minimum pourx=−b2ax=-\frac{b}{2a}x=−2ab
-
GGabie971 dernière édition par
Ah merci j'ai tout compris, Je trouve : f a son minimum pour X= 15\4 = 3.75. Par conséquent, la position du point M pour que l'aire du quadrilatère MNPQ soit minimale est à 3.75cm
Es-ce correct ?
-
mtschoon dernière édition par mtschoon

C'est bon mais précise que que M est à 3.75cm du point A
-
GGabie971 dernière édition par
D'accord merci beaucoup à bientot
-
mtschoon dernière édition par

De rien !
A+
-
Amalia dernière édition par
@mtschoon mais pourquoi on fait +50 ? Alors que avant ça on a fait -50....
 je suis perdue là..
je suis perdue là..
-
@Amalia Bonjour,
Que veux tu dire quand tu écris "Alors que avant ça, on a fait -50" ?
-
mtschoon dernière édition par mtschoon

@Amalia , bonjour,
Je pense que tu as suivi la discussion ouverte par @Gabie971 (qui date de plus 5 ans...) , et que tu as compris la démarche.
50 est l'aire, en cm², du carré ABCD
L'aire MNPQ s'obtient en soustrayant, à l'aire ABCD, l'aire des 4 triangles rectangles des "coins"
aire(MNPQ)=f(x)=50−x(10−x)−x(5−x)aire(MNPQ)=f(x)=50-x(10-x)-x(5-x)aire(MNPQ)=f(x)=50−x(10−x)−x(5−x)
f(x)=50−10x+x2−5x+x2=50−15x+2x2f(x)=50-10x+x^2-5x+x^2=50-15x+2x^2f(x)=50−10x+x2−5x+x2=50−15x+2x2
En ordonnant suivant les puissances décroissantes de x ( pour avoir la forme usuelle d'un polynôme du second degré)
f(x)=2x2−15x+50\boxed{f(x)=2x^2-15x+50}f(x)=2x2−15x+50
Reposte si besoin.
-
mtschoon dernière édition par mtschoon

Un schéma pour plus de clarté
En cm,
AB=CD=10
BC=DA=5
AM=BN=CP=DQ=x
MB=DP=10-x
CN=AQ=5-x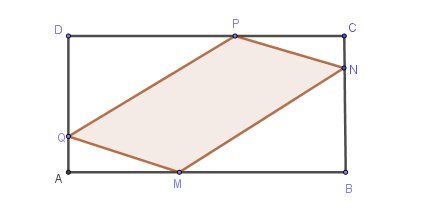
-
Amalia dernière édition par
@mtschoon ah ouii merci beaucoup ! Je viens de comprendre !
-
mtschoon dernière édition par

De rien @Amalia .
A+