forme polaire d'un nombre complexe 1

bonjour ce matin nous avons fait le cours sur l'argument d'un nombre complexe, personne n'a compris.....

pour la forme polaire de z= -1+j√3 j'ai trouvé (2; 2pi/3)

mais pour la forme polaire de z=2-2j√3/√3+j je bloque totalement.

merci par avance de votre aide.

Bonsoir dut,

As tu calculé le module du numérateur, du dénominateur ?

Bonsoir Noemi,
merci de votre réponse.
non je n'ai rien fait car je ne sais pas quoi et comment faire

donc calcule le module et l'argument du numérateur puis du dénominateur.

le seul problème c'est que je ne sais pas faire j'ai découvert ça ce matin.

pour 2 - 2√3 j

module √(2²+(-2√3)²) = 4
argument
cos a = 2/4 = 1/2 et sin a = -2√3/4 = -√3/2
donc arg = -π/3

applique le même raisonnement pour √3 + j

pour √3+j

module √(√3)^2+1^2=5
arg: cos =√3/5 sin:1^2/5

Vérifie le calcul du module 3+1 = 4 et √4=...

√4 ça fait 2

Calcule l'argument.

Bonsoir Noémi et dut.

Je ne fais que passer!

Lorsque dut aura fini la version proposée (très bonne, bien sûr), il pourra peut-être, pour s'entraîner, en faire une autre ( plus simple il me semble, vu qu'il débute le cours)

$z=2−23j3+j=(2−23j)(3−j)(3+j)(3−j)=...=−8j4=−2jz=\frac{2-2\sqrt 3j}{\sqrt 3+j}=\frac{(2-2\sqrt 3j)(\sqrt 3-j)}{(\sqrt 3+j)(\sqrt 3-j)}=...=\frac{-8j}{4}=-2j$

La forme polaire de -2j est facile à trouver.

Bonjour Noemi et mtschôn,
Merci de votre aide.
Je trouve la méthode de mtschoon beaucoup plus accessible à mon niveau.
Par contre je ne comprend pas l'opération : -2j c'est quoi.
Une fois que j'aurais trouver la forme polaire de -2j le calcul sera fini?

Merci et bonne journée.

Oui,

Si tu calcules la forme polaire de -2j tu auras répondu à la question;

Merci énormément.
Je vais essayer de le faire ce soir.
Pourrais je vous donner ma réponse pour vérification?

Oui,

Tu peux proposer ta réponse pour vérification.

j'arrive à faire √2^2+1^2 ca qui me donne √5 mais je suis bloque

Si tu parles de z=-2j, tu fais une erreur

$z = - 2 j = 0 + (- 2) j$

le module de z vaut $02+(−2)2=0+4=4=2\sqrt{0^2+(-2)^2}=\sqrt{0+4}=\sqrt 4=2$

2 n'est pas la forme polaire de 2-2√3j/√3j?

2 est le MODULE de z

Il faut que tu trouves unARGUMENT

Principe (mais regarde ton cours, car j'ignore l'explication donnée en cours)

Soit θ un argument de z

$cosθ=02=0cos\theta=\frac{0}{2}=0$

$sin⁡θ=−22=−1\sin\theta=\frac{-2}{2}=-1$

Tu en déduis θ

La forme polaire de z est (2,θ)

Je regarderai,sur internet comment faire pour trouver l'argument.
Merci et très bonne soiree

Connaissant le cosinus et le sinus de l'angle, tu n'as pratiquement rien à faire , regarde peut-être ton cours...ou fais le cercle trigonométrique (si tu connais)

Bonne soirée.

en regardant le peu de cours que j'ai je trouve:

(2; -pi/3

-∏/3 est faux

Tu es arrivé à trouver la forme polaire de z= -1+j√3 et tu ne trouves pas celle de 0-2j qui est plus simple...c'est bizarre.

Explique ta méthode pour que l'on comprenne ton erreur.

sur le cours il a noté " si x=0 et y<0 alors -∏/2
il y a aussi marqué ∏/2(90°)sin=1 et cos=0

Dans les reponses donées n'ayant -∏/2 mais -∏/3 j'en ai deduit que la réponse etait ca.

je suis perdu et j'ai envie de pleurer, le cours est très generaliste j'ai 6 questions notées à faire pour la prochaine fois et je ne sais pas comment faire car les exemples du cours ne correspondent pas au exercices demandés.

Pas de panique ! Tu y arriveras.

C'est -∏/2 l'argument car tu es dans le cas "si x=0 et y<0" mais cela doit correspondre à un graphique .
(et dans ce cas, il devrait y avoir écrit -∏/2(-90°) sin=-1 et cos=0

Regarde le graphique et comprends le . Tout s'éclairera.

z=-2j=0+(-2)j

z est de la forme x+yj avec x=0 et y=-2

L'image du nombre complexe z ( dans un repère orthonormé $(o,u⃗,v⃗)(o,\vec{u},\vec{v})$ du plan) est le point M de coordonnées (0,-2)

Place ce point M(0,-2)

Tu dois "voir" que la distance OM ( qui est le "module" de z) vaut 2

Tu dois "voir" qu'une mesure de l'angle $(u⃗,om⃗)(\vec{u},\vec{om})$ (qui est un argument de z) vaut -90° c'est à dire -∏/2

c'est vraiment gentil de croire en moi car c'est vrai que je suis en train de me décourager.

sur le peu que j'ai compris j'ai aussi trouvé (2; -∏/2) le problème c'est que dans les réponses du QCM il n'y a pas -∏/2.

Cela me gène que vous passiez dans de temps à essayer de m'expliquer mais sachez que je vous en suis énormément reconnaissant.

Un angle orienté à uneinfinité de mesures.

-∏/2 est la plus simple (on appelle ça la "mesure principe de l'angle")

Au lieu de -∏/2, il y a peut-être écrit 3∏/2 (270°)(qui est la plus petite mesure positive).

Il faut que tu comprennes pourquoi (en connaissant le sens trigonométrique "positif" conventionnel (sens inverse des aiguille d'une montre).

Je te joins un schéma (pas génial, mais c'est mieux que rien...) pour le cas où ça peut t'éclairer.

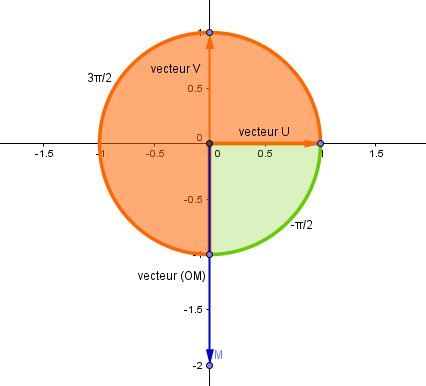
$fichier math$

Bonne réflexion.

non aucune reponse ne ressemble à ca.

les reponses sont (2; 2∏/3) ; (-2; -∏/3); (2;-∏/3)
il y a donc une erreur dans les réponses?

C'est super gentil, merci de votre aide; je travaillerais tant que je n'ai pas compris

Si tu n'as pas fait d'erreur en écrivant ton énoncé ( vérifie tout de même), z se simplifie en -2j

La forme polaire de -2j peut s'écrire (2,-∏/2), ou (2,3∏/2) par exemple, ce qui revient au même, mais certainement pas avec les réponses que tu proposes.

Regarde le graphique que je t'ai joint pour t'en apercevoir.

Merci pour toute votre aide.

De rien !

Un conseil peut-être : regarde bien ton cours et essaie de préciser, dans la dernière discussion que tu as ouverte, les propriétés que tu connais sur les formes polaires, pour pouvoir t'aider efficacement.