Fonction dérivé et trigonométrie

Bonjour, j'ai un long exercice à faire, pouvez-vous m'aider à la faire ?

Soit f [0;π/2] → ℜ

x → sin(2x)

a) Etudier les variations de f. (j'ai pensé à étudier les variations de sa fonction dérivée...)
b)Soit C un demi-cercle de centre E et de diamètre [JK], de rayon 2cm. Soit A un point de C tel que l'angle (JEA) = x avec ∈ [0;π/2].

À partir de A on construit le rectangle ABCD inscrit dans le demi-cercle C.

Soit S(x) l'aire du rectangle ABCD en cm² :

c) Montrer que s(x)=4f(x)
d) Pour quelles valeurs de S(x) est-elle maximale? Et quelle est cette valeur?
e)Pour quelles valeurs de x l'aire du rectangle ABCD est-elle limitée de l'aire maximale?

Bonjour alithekpop,

a) Calcule la dérivée de f, puis étudie son signe et construis le tableau de variation.

a) f(x)=sin(2x)

(ici sin(x) est dérivable sur ℜ et 2x est dérivable sur ℜ donc Ddr = ℜ)

f'(x) = cos(2x) * 2

Je n'ai jamais étudiée les variations d'une fonction cosinus ou sinus, je ne sais pas comment continuer ?

Cherche le signe de cos(2x) pour x variant de 0 à π/2.

Ici, cos(2x) est positif pour x variant de 0 à π/2.

Donc, cos(2x) > 0

?

Pour x variant de 0 à π/2,
2x varie de 0 à π
et cos (2x) varie de -1 à 1
et cos(2x)= 0 si x = π/4
donc
pour x variant de 0 à π/4 cos(2x) ....
pour ....

Je ne comprends absolument pas ?

(Pour passer de x à 2x qui varie, vous avez multiplié 0 et π/2 par 2 ?)

Et d'où vient le π/4 ?

Oui pour passer de x à 2x on multiplie par 2
donc si x varie de 0 à π/2
2x varie de 20 à 2π/2

Tu dois savoir que cos (π/2) = 0,
donc si x = π/4, 2x = π/2
ou tu résous l'équation cos(2x) = 0 soit = cos(π/2)

Je commences progressivement à comprendre les démarches à suivre!
Que dois-je faire à ce stade-là?

Construis le tableau de variation.

Voici ce que j'ai trouvé :

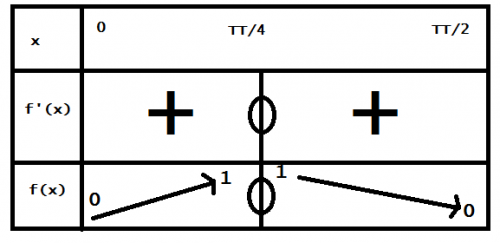
$fichier math$

Deux erreurs,

Pour le signe de la dérivée : lle + à droite qui doit être un moins et
pour les variations de f : le 0 au centre qui est en trop.

Je vais modifier...quelques fautes d'inattention...

$fichier math$

C'est correct,

Au lieu de f'(x) tu peux noter : signe de f'(x)
et au lieu de f(x) tu peux noter : variation de f

C'est noté.

Pour la b), voici ma figure :

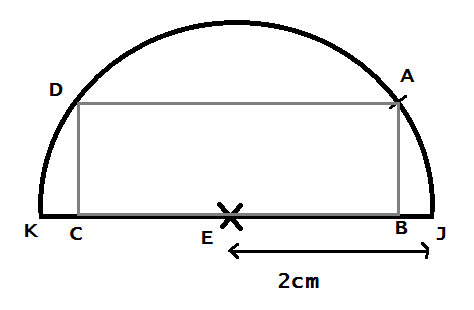
$fichier math$

est-ce bien cela ?

La figure est correcte, calcule l'aire du rectangle.

Je dois exprimer cette aire en fonction de x ?

oui en fonction de sin x et cos x
AB = 2 sin x
BE = ....

puis tu utilises la relation sin x cos x = .....

AB = 2 sin x
BE = 2 cos x ?

Notre professeur nous a indiqué une formule : Sin(2x) = 2 sin(x) cos(x), mais je n'arrive pas à m'en servir, je ne tombe pas sur 4sin(x) ?

l'aire du rectangle c'est 4 x AB x BE / 2, soit 2 AB x BE
= ....

Cela fait :

4 × ( 2 cos (x) sin (x) ) = 4 sin (2x) ?

Oui

donc 4 f(x)

J'étudie de nouveau les variations de la fonction dérivée de 4 sin( 2x) pour la d) ?

Non

Tu reprends le résultat de la question a : x = π/4

Logiquement comme sin (2x) a pour maximale 1 pour x = π/4; ici c'est 4 car la fonction est 4 sin(2x).

Oui

le maximum est 4

La e) je ne comprends pas le sens de la question ?

Tu as trouvé x =π/4,

y a t-il une autre valeur de x telle que l'aire du rectangle soit maximale ?
Une autre position du point A ?

Non, il ne devrait pas en avoir ?

Il s'agit de résoudre sin(2x) = 1

Je ne sais pas du tout comment résoudre cela ?

Bonjour,

J*e n'ai pas lu ce long topic...

allthekpop, je regarde seulement ta dernière question

sin(2x) = 1, car Noemi n'a pas dû la voir.*

En utilisant le cercle trigonométrique, tu n'as rien à faire (ou presque)
Il y a un seul angle dont le sinus vaut 1 (c'est l'angle droit direct).

sin(2x)=1 <=> 2x=∏/2+2k∏ <=>x=∏/4+k∏ , avec k ∈ Z

Evidemment, tu peux faire plus compliqué :

sin(2x)=1 <=> sin(2x)=sin(∏/2)

Ensuite, tu utilises ton cours ;

sina=sinb <=> a=b+2k∏ ou a=∏-b+2k∏ , avec k ∈ Z

Après calculs, tu trouveras pareil.

Après attente je l'avais déjà faite voici ce que j'ai trouvée pour le e) :

s(x) = 4 f(x) = 4 × sin (2x)

4 × sin(2x) = 4/2

sin (2x) = 1/2

Donc 2 x =TT/6 ou 2x = 5 TT / 6 mais 5TT/6 ∉ [0;π/2)

Donc x = TT / 12

?

Pour la e), pouvez-vous m'indiquer si c'est bien cela ou si ce n'est pas cela ?

merci

2x = π/6 donne x = π / 12
et
2x = 5π/6 donne x= 5π/12
Donc
....

Donc l'aire ABCD est limitée de l'aire maximale pour x = π/12 donc pour x = π/4 - 1/6 π.

Merci de bien répondre à ma réponse s'il vous plait...

allthekpop
Donc l'aire ABCD est limitée de l'aire maximale pour x = π/12 donc pour x = π/4 - 1/6 π.

Cette réponse est peu claire !!

Alors l'aire ABCD est limitée de l'aire maximale pour x = π/12 ?

Je ne vois pas quoi rajouter d'autre à cela.

Après relecture de l'énoncé

d) S(x) est maximale si sin(2x) = 1 ce qui donne S(x) = 4
e) résoudre sin(2x) = 1
donc 2x = π/2 + 2kπ
d'ou x = π/4 vu que x appartient à [0;π/2]