Résoudre une équation et représenter les solutions sur le cercle trigonométrique

Bonjour !

Il y a un exercice qui me pose problème, pouvez-vous m'aider ?

Soit l'équation :

[ Sin (x) ] ² = 1/2

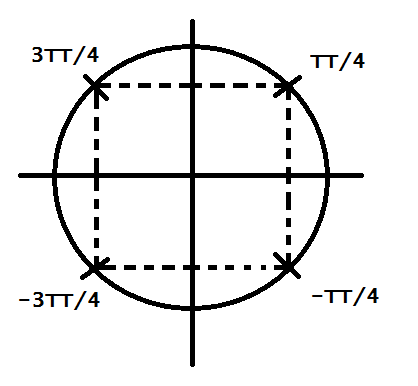
1) Résoudre l'équation suivante dans [-π;π] et représenter les solutions sur le cercle trigonométrique.
2) Montrer que les solutions définissent des points qui forment un carré.

Voici mes réponses :

sin(x)² = 1/2
⇔ sin(x) = √1/2 ou -√1/2

$fichier math$

(Je ne suis pas certaine de cette réponse)

Comme π = 180°

π/4 = 45 °
3π/4 = 135 °
-π/4 = - 45°
-3π/4 = - 135°

Or si on place notre rapporteur au centre d'un carré, ses quatre points sont désignés par les valeurs ci-dessus. Les solutions définissent donc des points qui forment un carré.

*J'ai remarqué que la valeurs de sin coïncide avec celles de cos seulement je ne sais pas comment l'exploiter :

sin π/4 = cos π/4 : √2/2 et √2/2
sin 3π/4 = cos 3π/4 : √2/2 et -√2/2
...*

Que pensez-vous de ma deuxième réponse ?

Merci..

Bonsoir alithekpop,

Pour la question 2, utilise une propriété du carré.
Par exemple avec les diagonales.

Puis-je utiliser mes valeurs de cosinus et de sinus pour prouver cela en utiliser cette propriété :

Si un parallélogramme a ses diagonales qui sont perpendiculaires et qui ont la même longueur, alors c’est un carré.

Car on nous demande de prouver que ces solutions définissent des points qui forment un carré ?

Bonjour,

Pour démontrer que sin(π/4) = cos(π/4) penser à la formule

cos²x + sin²x = 1

Et pour retrouver les sin et cos des angles remarquables voir la fiche : http://www.math...ours-92.html

Oui mais je ne comprends pas comment cela pourrait démontrer une telle figure ?

Tu peux utiliser la propriété que tu as indiquée.

Merci !