Calcul de distance de freinage
-
Nnassou30 dernière édition par lisaportail
Bonsoir,
**On considère un véhicule dont la distance de freinage sur route sèche (en mètres) est donnée par :
Ds(v) = 0.005v² + 0.27v -----) où v est exprimée en km.h-1A/ quel panneau de limitation doit-on placer dans une rue où l’on souhaite que ce véhicule ait une distance d’arrêt inférieures à 15 m sur route sèche ?
B/ Sur route mouillée, la distance de freinage de ce véhicule est :
Dm(v) = 0.007v² + 0.27v**Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
(15 - 0.27) / 0.005 = v²
v = √2946
= 54.27 mA/ panneau à 60 km/h
Ds(v) = 0.007v² + 0.27v
15 = 0.007v² + 0.27v
(15 - 0.27) / 0.007 = v²
v = √2104.28
= 45.87 mmerci pour votre aide.
-
Nnassou30 dernière édition par
Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
V(0.005V + 0.27) – 15 = 0Ds(v) = 0.007v² + 0.27v
15 = 0.007v² + 0.27v
0.007v² + 0.27v - 15 = 0
V(0.007V + 0.27) – 15 = 0Est-ce que je suis sur la bonne voie ? par contre je suis coincée à ce niveau.
-
Bonsoir nassou30,
Le début est juste
Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0,005v² + 0,27v - 15 = 0Résous cette équation du second degré
soit en factorisant soit avec le calcul du discriminant
-
Nnassou30 dernière édition par
Bonsoir Noémi.
Merci d'être là.
Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0,005v² + 0,27v - 15 = 0Calcul du discrminant
Δ = (0.27)2 − (4 × 0.005 × -15) = 0.0729 + 0.3
Le discriminant est égal à 0.3729Est-ce correct si oui que dois-je faire après ?
-
C'est correct.
delta positif donc deux solutions qu'il faut que tu calcules.
-
Nnassou30 dernière édition par
Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
V(0.005V + 0.27) – 15 = 0
Δ = (0.27)2 − (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.Ds(v) = 0.007v² + 0.27v
15 = 0.007v² + 0.27v
0.007v² + 0.27v - 15 = 0
V(0.007V + 0.27) – 15 = 0
Δ = (0.27)2 − (4 × 0.007 × -15) = 0.0729 + 0.42 .
Le discriminant est égal à 0.4929.
-
C'est aussi 15 m sur route mouillée ?
-
Nnassou30 dernière édition par
Et zut et je vous prie de m'en excuser, j'ai oublié de rajouter à la question
B/ Sur route mouillée, la distance de freinage de ce véhicule est :
Dm(v) = 0.007v² + 0.27vA quelle distance de freinage sur route mouillée est elle 20% supérieure à celle sur route sèche ?
j'ai remplacé 20% par 1.2 donc
Ds(v) = 0.007v² + 0.27v
1.2 = 0.007v² + 0.27v
0.007v² + 0.27v + 1.2 = 0
Δ = (0.27)2 − (4 × 0.007 × 1.2) = 0.0729 − 0.0336 .
Le discriminant est égal à 0.0393.
-
Sur route mouillée, ce n'est pas 1,2 mais 15 x 1,2 = ...
Calcule ensuite x1 et x2
x1 = (-b-√delta)/2a
x2 = ....
-
Nnassou30 dernière édition par
Bonsoir Noemi,
0.007v² + 0.27v + (15 x 1.2 ) = 0
Δ = (0.27)2 − (4 × 0.007 × 18) = 0.0729 − 0.504 .
Le discriminant est égal à -0.4311.L'équation n'admet aucune solution réelle, car Δ < 0.
-
Attention
c'est :
0.007v² + 0.27v - (15 x 1.2 ) = 0
-
Nnassou30 dernière édition par
0.007v² + 0.27v + (-15 x 1.2 ) = 0
0.007v² + 0.27v -18 = 0
Δ = (0.27)2 − (4 × 0.007 × -18) = 0.0729 − 0.504 .
Le discriminant est égal à -0.5769L'équation n'admet aucune solution réelle, car Δ < 0.
v1 = -135 - 15x √641 / 7
v2 = -135 + 15x √641 / 7
-
Non
delta = +0.5769
vérifie le calcul pour V1 et V2
-
Nnassou30 dernière édition par
Zut delta est bien égale à + 0.5769
0.007v² + 0.27v + (-15 x 1.2 ) = 0
0.007v² + 0.27v -18 = 0
Δ = (0.27)2 − (4 × 0.007 × -18) = 0.0729 + 0.504 .
Le discriminant est égal à 0.5769L'équation admet 2 solutions , car Δ < 0.
v1 = -135 - 15x √641 / 7 = -73.53
v2 = -135 + 15x √641 / 7 = 34.97
-
Comment trouves tu ces valeurs pour le calcul de V1 et V2 ?
Bonne nuit
-
Nnassou30 dernière édition par
merci beaucoup et Bonne nuit, à demain.
-
Nnassou30 dernière édition par
Bonsoir
,Ds(v) = 0.005v² + 0.27v
15 = 0.005v² + 0.27v
0.005v² + 0.27v - 15 = 0
Δ = (0.27)2 − (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.
L'équation admet 2 solutions réelles, car Δ > 0.v1 = -27 - √3729
v2 = -27 + √37290.007v² + 0.27v + (-15 x 1.2 ) = 0
0.007v² + 0.27v -18 = 0
Δ = (0.27)2 − (4 × 0.007 × -18) = 0.0729 − 0.504 .
Le discriminant est égal à -0.5769L'équation n'admet aucune solution réelle, car Δ < 0.
v1 = -135 - 15x √641 / 7
v2 = -135 + 15x √641 / 7merci de m'indiquer les démarches à suivre.
-
Je corrige sur ta réponse. Vérifie les calculs
0.005v² + 0.27v - 15 = 0
Δ = (0.27)² − (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.
L'équation admet 2 solutions réelles, car Δ > 0.v1 = (-0,27 - √0,3729)/(2x0,005) = -88,07
v2 = (-0,27 + √0,3729)/(2x0,005) =34,07Conclusion
....Je corrige sur ta réponse
0.007v² + 0.27v + (-15 x 1.2 ) = 0
0.007v² + 0.27v -18 = 0
Δ = (0.27)² − (4 × 0.007 × (-18)) = 0.0729 − 0.504 .
Le discriminant est égal à 0.5769L'équation admet deux solutions réelles, car Δ > 0.
v1 =( -0,27 - √0,5769) / (2x0,007) = -73,54
v2 =( -0,27 + √0,5769) / (2x0,007) = 34,97
conclusion
....
-
Nnassou30 dernière édition par
Bonsoir Noemi,
0.005v² + 0.27v - 15 = 0
Δ = (0.27)² − (4 × 0.005 × -15) = 0.0729 + 0.3 .
Le discriminant est égal à 0.3729.
L'équation admet 2 solutions réelles, car Δ > 0.v1 = (-0,27 - √0,3729)/(2x0,005) = -88,07
v2 = (-0,27 + √0,3729)/(2x0,005) =34,07S = ] 0 ; 34.07 ]
On doit placer un panneau limitant la vitesse à 30 km/h,
Je corrige sur ta réponse
0.007v² + 0.27v + (-15 x 1.2 ) = 0
0.007v² + 0.27v -18 = 0
Δ = (0.27)² − (4 × 0.007 × (-18)) = 0.0729 − 0.504 .
Le discriminant est égal à 0.5769L'équation admet deux solutions réelles, car Δ > 0.
v1 =( -0,27 - √0,5769) / (2x0,007) = -73,54
v2 =( -0,27 + √0,5769) / (2x0,007) = 34,97S = ] 0 ; 34.07 ]
-
Oui,
conclue aussi pour la deuxième question.
-
Nnassou30 dernière édition par
Merci,
j'ai l'impression qu'il y a quelque chose qui cloche, je ne peux pas avoir le même résultat, sur route sèche et sur route mouillée.
Est ce que je dois rajouter encore les 20% ?
-
Sur route mouillée tu as trouvé 34,97 km/h.
-
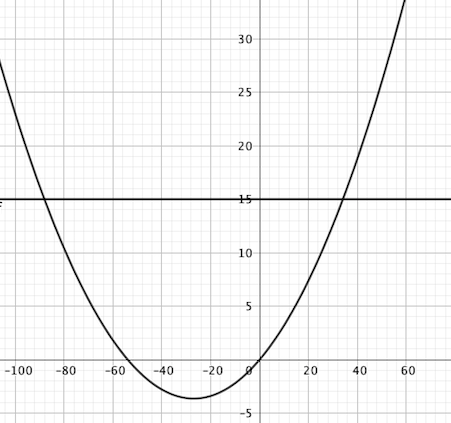
MMathis.L dernière édition par
Bonjours, serez vous tracer la courbe de la fonction ds et donc répondre à la question 1 graphiquement et algébriquement (par calcul)?
Merci
-
Mathis.L Bonjour,
La courbe est une parabole. Graphiquement, tu obtiendras une valeur approchée. Le calcul est indiqué dans la première partie.
-
MMathis.L dernière édition par
Merci beaucoup,
cependant je ne comprend pas, quand je tape la formule sur ma calculatrice j'obtient une droite
-
Modifie la fenêtre de la calculatrice.
Par exemple x variant de -100 à 60 et y de -5 à 30.
-
MMathis.L dernière édition par
@Noemi a dit dans Calcul de distance de freinage :
-100 à 60 e
en faite j'ai ecris sur ma calculatrice : 0.005x2+0.27x
-
BBlack-Jack dernière édition par
@Noemi a dit dans Calcul de distance de freinage :
Sur route mouillée tu as trouvé 34,97 m
Bonjour,
Attention, en plusieurs endroits dans ce topic, il y a confusion entre la vitesse et la distance.
Sur route mouillée ... 34,97 km/h
-
@Mathis-L
Donc n'oublie pas d'élever au carré.
-
MMathis.L dernière édition par
@Black-Jack donc le panneau de limitation reste 30km/h sur route mouillé?
-
Oui c'est bien une limitation à 30 km/h pour les deux cas.
-
MMathis.L dernière édition par
@Noemi merci
-
@Black-Jack Bonjour,
Merci pour la rectification.
-
MMathis.L dernière édition par
@Noemi Mais a la question 2 on nous demmande pas le panneau de limitation, mais à quelle vitesse la vitesse de freinage sur route mouillé est est elle 20% plus eleve quesur route sèche?
Moi j'ai trouvé 54km/h
-
Je suppose que tu as voulu écrire : "distance de freinage sur route mouillée est 20% ....".
La réponse est bien 54 km/h
-
MMathis.L dernière édition par
@Noemi merci bien
-
MMarcitchnik_ dernière édition par
@Noemi Elle serait-plutot pas de 53 ? (34.97 + 18 ≈ 53)
-
Il faut résoudre l'équation Dm=1,2DsD_m= 1,2 D_sDm=1,2Ds en utilisant les expressions avec la vitesse.
-
MMarcitchnik_ dernière édition par
Dm = 1.2Ds
Donc Dm = 1.2 x 34.07
C'est ca ?
-
MMarcitchnik_ dernière édition par
mais j'obtiens 40.884, je suis coincé
-
Yyasir dernière édition par
T est coincé??
-
MMarcitchnik_ dernière édition par
Comme j'ai déjà écrit, je comprend pas comment vous avez trouver 54 : moi, j'ai additionner 34.97 + 18 = environ 53 donc qui est proche de 54, ou alors il faut bien trouver 54 et je sais pas comment
-
MMarcitchnik_ dernière édition par
Si quelqu'un peut me conseiller quoi faire pour trouver le résultat, je serai très reconnaissant.
-
J'ai indiqué l'équation à résoudre.
-
MMarcitchnik_ dernière édition par
@Marcitchnik_ a dit dans Calcul de distance de freinage :
1.2 x 34.07
-
Il faut résoudre l'équation Dm=1,2DsD_m= 1,2 D_sDm=1,2Ds en utilisant les expressions avec la vitesse.
Soit 0,007v2+0,27v=1,2(0,005v2+0,27v)0,007v^2+0,27v=1,2(0,005v^2+0,27v)0,007v2+0,27v=1,2(0,005v2+0,27v)
-
MMarcitchnik_ dernière édition par
J'ai 0.007v² + 0.27v = 0.00003v² + 0.08748v
-
CCyprien Delion dernière édition par
Ce message a été supprimé !
-
AAlfred dernière édition par
Bonsoir, Pouvez vous écrire ce que l'on doit écrire dans la copie ?
-
MMarcitchnik_ dernière édition par
Pour quel exercice ?
-
@Alfred Bonsoir,
Ce site n'a pas pour vocation de faire les exercices à votre place.
L'objectif principal est de vous donner des pistes et de corriger éventuellement vos éléments de réponse.
Pour trouver la vitesse;
Il faut résoudre l'équation Dm=1,2DsD_m= 1,2 D_sDm=1,2Ds en utilisant les expressions avec la vitesse.
Soit 0,007v2+0,27v=1,2(0,005v2+0,27v)0,007v^2+0,27v=1,2(0,005v^2+0,27v)0,007v2+0,27v=1,2(0,005v2+0,27v)
0,007v2+0,27v=0,006v2+0,324v0,007v^2+0,27v = 0,006v^2+0,324v0,007v2+0,27v=0,006v2+0,324v
0,001v2=0,054v0,001v^2=0,054v0,001v2=0,054v avec vvv différent de 0.
0,001v=0,0540,001v=0,0540,001v=0,054
v=0,0540,001=.....v= \dfrac{0,054}{0,001}= .....v=0,0010,054=.....
ne pas oublier l'unité.
-
MMarcitchnik_ dernière édition par Marcitchnik_
D'accord, j'avais mal calculer 1,2(0,005v2+0,27v), merci beaucoup pour votre aide, je ferais d'avantage attention prochainement