logarithme népérien Algorithme

Bonjour, voilâ déjà deux jours que je creuse mais je n'arrive pas à continuer ce DM de maths :

f(x)=3 ln (626-x²)

1/ Déterminer l'ensemble D de définition de la fonction f

J'ai répondu ]-√626; √626[

2/ Etabir le tableau de variation de f sur D (limites comprises)

Je trouve problème de définition en -√626 et √626 puis croissante de -√626 (lim =-∞) à 0 (=19.3) puis décroissante de 0 à √626 (lim = -∞)

3/ Déterminer 'intervalle I (inclus dans D) des valeurs de x pour lesquelles f(x)≥0

Je bloque totallement car sur la calculatrice je ne trouve pas de nombre assurant le passage d'un nombre négatif à positif pourtant d'après les limites il devrait y en avoir ...

Merci de votre aide

Bonjour,

Tu peux peut-être commencer par regarder ici, vers la page 5 (Travaux pratiques TP Algorithme2)

http://jgaltier.free.fr/Terminale_S/Corriges/chapitre_6.pdf

Reposte si besoin.

Merci beaucoup !
Cependant je n'arrive pas à comprendre l'algorithme pourriez vous m'expliquer comment faire ?

Quelle est la question ?

Il faut que tu donnesl'énoncé de la questionrelative à cet algorithme pour que l'on sache précisément de quoi il s'agit.

On souhaite mesurer la longueur de l'armature d'un abri de piscine ayant la forme de la fonction restreinte à l'intervalle I (l'unité étant 1dm). On note L la valeur exacte de la longueur recherchée de l'armature. On partage l'intervalle [-25;25] en n intervalles d'amplitude p=50/n et on considere les points Ak de la courbe f d'abscisse -25+kp ou k est un entier tel que 0≤k≤n
On note Sn = A0A1+A1A2+...+An-1An

3-a Recopier et completer l'algo suivant pour obtenir une valeur approchée de Sn pour un entier naturel non nul donné

Saisir n
p prend la valeur 50/n
x prend la valeur -25
S prend la valeur 0
Pour k alalnt de 0 à n-1 faire
d prend la valeur √.......
S prend la valeur S+
x prend la valeur x+
Fin pour Afficher S

A partir de la racine je ne vois pas quoi mettre? Pourriez vous m'aider merci

Pour k allant de 0 à n-1

$< s t r o n g > d = A$ k $A</em>{k+1}$

Pour calculer d , il faut utiliser le théorème de Pythagore ou la formule de la distance (ce qui revient au même)

Je te mets un schéma pour plus de clarté.

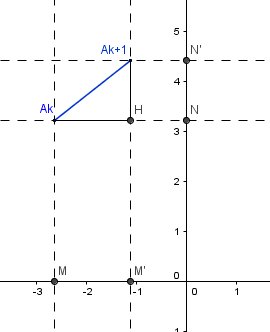
$fichier math$

Calculs :

$\text{d^2=a_ka_{k+1}^2=a_kh^2+ha_{k+1}^2=mm'^2+nn'^2$

L'abscisse de M est x
L'abscisse de M' est x+p
$\text{mm'=x+p-x=p$

L'ordonnée de N est f(x)
L'ordonnée de N' est f(x+p)
$\text{nn'=f(x+p)-f(x)$

D'où

$\text{d^2=p^2+(f(x+p)-f(x))^2$

$\text{\fbox{d=\sqrt{p^2+(f(x+p)-f(x))^2}}$

Complément pour les 2 dernières lignes de l'algorithme :
S prend la valeurS+d
x prend la valeurx+p

Merci beaucoup !

Par contre j'aurais encore une dernière question qu'est ce que représente N N' et M M' car dans l'énoncé ces lettres ne figurent pas ? Car je voudrais expliquer comment obtenir la formule mais je ne comprends pas ce que représente ces lettres ? Merci beaucoup

L'axe passant par 0 et "vertical" est l'axe des ordonnées.
N est le projeté orthogonal de $A_k$ sur l'axe des ordonnées
N' est le projeté orthogonal de $A_{k+1}$ sur l'axe des ordonnées

L'axe passant par 0 et "horizontal" est l'axe des abscisses.
M est le projeté orthogonal de $A_k$ sur l'axe des abscisses
M' est le projeté orthogonal de $A_{k+1}$ sur l'axe des abscisses

J'ai mis des lettres pour t'expliquer la formule de la distance d

Ah oui d'accord c'est plus clair comme cela !
Merci beaucoup pour le temps que vous m'avez accordé
Bonne soirée !

De rien !

Bon travail.