Calculs dans un repère, vecteurs et équations

Bonsoir,

Je reviens donc ici pour vous demandez votre aide pour le dernier exercice de mon devoir maison...
J'ai donc écrit le sujet, et mes réponses/essaies en gras. (ainsi qu'une photo de mon graphique pour le moment).

Une figure sera faite et complétée tout au long de l'exercice. Dans un repère orthonormé (O;I;J), on donne les points A(-1;3), B(4;0), C(2;-5).

Calculer la distance AB

√(xb-xa)²+(yb-ya)²
AB=√(4-(-1)²+(0-3)²
=√(5)²+(-3)²
=√(25+(-9)
=√16
=4

Calculer les coordonnées de AB

(xb-xa ; yb-ya)
AB=(4-(-1) ; 0-3)
=(5;-3)

Soit I le milieu de [AC]. Calculer les coordonnées de I et en déduire les coordonnées du point D tel que ABCD soit un parallélogramme.

**xm=(xa+xc)÷2 --- ym=(ya+yc)÷2
=((-1)+2)÷2 --- =(3+(-5))÷2
=0,5 --- =-1

I (0,5;-1)**

Mais par contre je ne sais pas du tout comment faire pour calculer les coordonnées du point D... J'ai pensé qu'il fallait donc aussi calculer la distance et les coordonnées de BC.

**Distance ; √(xc-xb)²+(yc-yb)²
BC=√(2-4)²+(-5-0)²
=√(4+25)
=√29
≈5,38

Coordonnées ; (xc-xb ; yc-yb)
BC=(2-4 ; -5-0)
=(-2;-5)**

E(7;3) et F(2;5). Est-ce que le quadrilatère AFEB est un parallélogramme ?
P est un point défini par la relation BP=AC+3÷2 BA, calculer les coordonnées de P. (il y a des flèches → sur BP, AC et BA)
Que peux-tu en conjecturer à propos des points D, P et C ? Prouve-le.
Déterminer par le calcul une équation de la droite (DA).
Déterminer par le calcul une équation de la droite d parallèle à (DA) qui passe par G(-4;2).
Soit d' la droite d'équation : y=-(2÷3)x-5. Construire d' et déterminer par lz calcul les coordonnées du point d'intersection des droites d et d'.

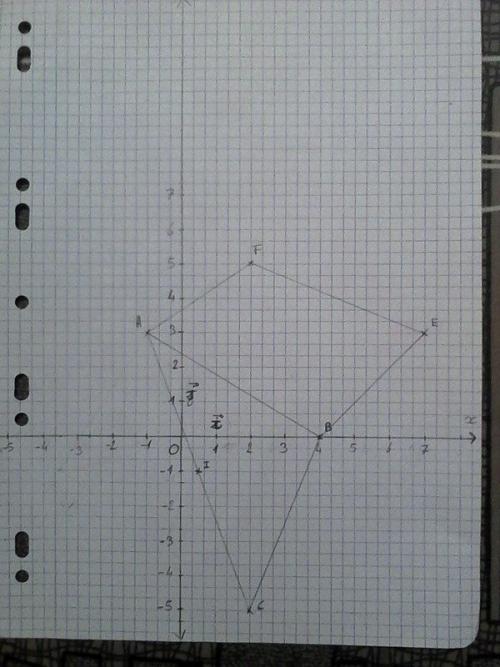
Graphique de l'exercice

Merci d'avance pour votre aide

Bonsoir Amélie,

(-3)² = 9 et non -9, rectifie le calcul de AB.
Pour les coordonnées du point D, le point I est le milieu du segment BI.
Compare les vecteurs AF et BE.

(-3)² = 9 ? Je viens de revérifier avec ma calculatrice et elle m'indique -9 comme résultat..
Oui je sais bien mais vu qu'il me manque les coordonnées de D, je ne sais pas comment faire...

As tu fait le calcul avec les parenthèses ?

Utilise vect BI = vect ID

Non je ne les avais pas mises...

Coordonnées du vecteur BI :
(xi-xb ; yi-yb)
=(0,5-4 ; -1-0)
=(-3,5;-1)

Coordonnées du vecteur ID :
(xd-xi ; yd-yi)
=(xd-0,5 ; yd-(-1))
=(...;...)

Milieu du segment AE :
xm=(xe+xa)÷2
=(7+(-1))÷2
=3

ym=(ye+ya)÷2
=(3+3)÷2
=3

M(3;3)

Milieu du segment BF :
xm=(xf+xb)÷2
=(2+4)÷2
=3

ym=(yf+yb)÷2
=(5+0)÷2
=2,5

M(3;2,5)

Comme les 2 segments ne se coupent pas en un même milieu, alors le quadrilatère AFEB n'est pas un parallélogramme.

Question 3
Coordonnées du vecteur BI :
(xi-xb ; yi-yb)
=(0,5-4 ; -1-0)
=(-3,5;-1)

Coordonnées du vecteur ID :
(xd-xi ; yd-yi)
=(xd-0,5 ; yd-(-1))
=(-3,5;-1)
tu résous
xd-0,5 = -3,5
et yd+1 = -1

Question 4 correcte.

Ce qui reviendrait donc au même que pour BI :
=(0,5-4 ; -1-0)
=(-3,5;-1)

Mais le problème est que même en ayant les coordonnées de ID (-3,5;-1), je ne sais pas comment faire pour juste avoir les coordonnées de D... Quelle formule je dois utilisé ou je ne sais pas...

tu résous
xd-0,5 = -3,5 soit xd = ...
et yd+1 = -1 soit yd = ....
donc D ....

Vérifie en plaçant le point D sur le schéma.

xd-0,5 = -3,5 soit xd = -3
et yd+1 = -1 soit yd = -2
donc D (-3;-2)

Ça correspond bien sur le schéma !

Pour la question 5 :
Comment dois-je faire pour calculer les coordonnées du point P ?
J'ai pensé qu'il était utile de calculer les coordonnées et les distances de AC et BA

Pour la question 5,
Calcule chacun des vecteurs puis utilise la relation.

'Comment' calculer ces vecteurs ?

Tout ce que j'ai déjà pu calculer, c'était ça :

Coordonnées de AC :
(xc-xa ; yc-ya)
=(2-(-1) ; -5-3)
=(3;-8)

Distance de AC :
√(xc-xa)²+(yc-ya)²
=√(2-(-1)²+(-5-3)²
=√(3)²+(-8)²
=√(9+64)
=√73
=8,54

Coordonnées de BA :
(xa-xb ; ya-yb)
=(-1-4 ; 3-0)
=(-5 ; 3)

Distance de BA :
√(xa-xb)²+(ya+yb)²
=√(-1-4)²+(3-0)²
=√(-5)²+(3)²
=√(25+9)
=√34
=5,83

vect AC ; (3;-8)
vect BA ; (-5.3)
AC+3/2(BA) = (3-15/2 ; ......)

vect BP; (xp -4 ; yp)

xp- 4 =
....

AC+3/2(BA) = (
3-15/2; ......)

Désolé mais je ne comprends pas d'où sort le 3 et -15/2...

vect AC ; (3;-8)
vect BA ; (-5.3)
vect AC + 3/2 vect BA ; (3 + (3/2)*(-5) ; -8 + (3/2)*3)
= ....

vect AC + 3/2 vect BA ; (3 + (3/2)*(-5) ; -8 + (3/2)*3)
= (-4,5 ; -3,5)

P(-4,5 ; -3,5)

BP = (xp -4 ; yp)
=(-4,5-4 ; -3,5)
=(-8,5 ; -3,5)

vect AC + 3/2 vect BA : (-4,5 ; -3,5)

BP = (xp -4 ; yp)
Soit
xp - 4 = -4,5 ; xp = ....
et
yp = -3,5

BP = (xp -4 ; yp)
Soit
xp - 4 = -4,5 ; xp = -0,5
et
yp = -3,5

BP(-0,5 ; -3,5) ?

xp - 4 = -4,5 ; xp = -0,5
et
yp = -3,5

Donc les coordonnées du point P (-0,5 ; -3,5)

Très bien merci !