Trouver la tangente d'une fonction avec logarithme népérien

Bonjour pouvez vous m'aider ?

J'ai une fonction : ln (x )/x
Sa dérivée : 1-ln (x)/x^2

Je dois trouver une tangente à la courbe Cf passant par l'origine du repère comment fait ?

Bonjour,

Piste,

Tu travailles sur ]0,+∞[

En un point d'abscisse a (a > 0), tu écris l'équation de la tangente (T) en ce point sous la forme

$y = f^{'} (a) (x - a) + f (a)$

Vu que (T) dois passer par O(0,0), tu remplaces, dans cette équation, x par 0 et y par 0

Tu obtiendras ainsi une équation d'inconnue a à résoudre.

C'est à dire que cela devient :

(1-Ln/x^2)(0-a)+lnx/x ?

Je trouve :

a=(x^2ln (x))/x-xln (x)

Est ce bien cela .

Tu sembles faire des confusions.

Equation de (T) :

$y=1−lnaa2(x−a)+lnaay=\frac{1-lna}{a^2}(x-a)+\frac{lna}{a}$

Tu remplaces maintenant x par 0 et y par 0

Et dans ce cas la je trouve pour le moment quelque chose de la forme :

-(a-alna)/a^2 + lna/a

Dois je continuer ?

Il te faux l'égalité :

0=....

Et bien sûr que tu continues !

Tu dois résoudre l'équation d'inconnue a obtenue pour trouver a.

Il te faux l'égalité :

0=....

Et bien sûr que tu continues !

Tu dois résoudre l'équation d'inconnue a obtenue pour trouver a.

À la fin je trouve -a^2/a^3 = 0
Donc -1/a = 0 et a = 0

?

Non, c'est faux.

$0=1−lnaa2(−a)+lnaa0=\frac{1-lna}{a^2}(-a)+\frac{lna}{a}$

Tu réduis au même dénominateur et tu simplifies.

Tu dois trouver :

$0=−a+2alnaa2↔−a+2alna=00=\frac{-a+2alna}{a^2} \leftrightarrow -a+2a lna=0$

Tu mets a en facteur et tu termines la résolution.

Si je met a en facteur j'ai :
a (-1+2lna)=0
a=0 ?

La factorisation est bonne mais a ne peut pas valoir 0 vu que a > 0
(tu travailles sur ]0,+∞[)

Il te reste à résoudre :

$- 1 + 2 l n a = 0$

Je trouve a=e^1/2

Est ce bien cela ?

Oui, c'est bon

$a=e12=ea=e^{\frac{1}{2}}=\sqrt e$

Maintenant que tu as la valeur de a satisfaisante, il te reste à remplacer a par cette valeur, pour donner l'équation de la tangente demandée.

A la fin de tes calculs, tu dois trouver, pour l'équation de la tangente satisfaisante :

$\fbox{y=\frac{1}{2e}x}$

Bons calculs !

Cela devient :

(1-lnx/x^2)(-√e)+lnx/x ?

Merci bien !

Par contre 1/2e^x graphiquement ça ne passe pas vers 0 (0,0) ?

Tu ne sembles pas avoir terminé las calculs correctement !

Réfléchis...

Une tangente est une droite ( passant par l'origine dans ton cas) , elle ne risque pas avoir l'équation que tu indiques !

Il s'agit de :

$y=(12e)xy=(\frac{1}{2e})x$

Equation de la forme
y=Ax(fonction linéaire) avec $a=12ea=\frac{1}{2e}$

Voici l'illustration graphique

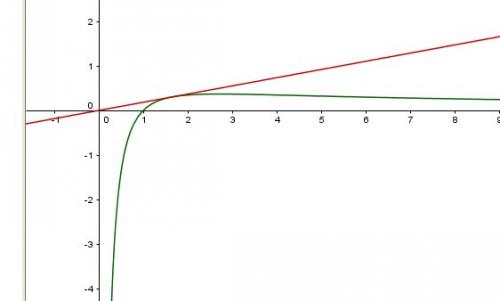
$fichier math$

Tout cela me semble beaucoup plus désormais donc je vais refaire mon calcul et voir si je tombe bien sur cela !

Je ne tombe pas sur ça ... Est ce bien (1-lnx/x^2)(x-√e)+lnx/x ? Si ce n'est pas le cas j'ai également essayée pour x=0 mais je tombe sur une fraction ! $fichier math$

Voici mon calcul pour x=0

Et voici mon autre calcul pour (x-√e) :

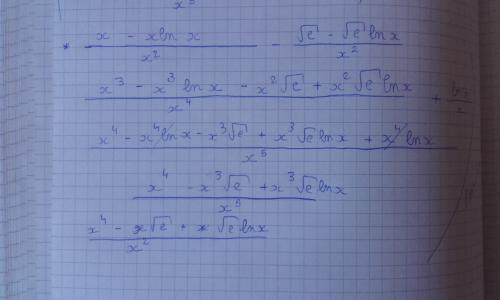
$fichier math$

Tu fais des confusions .

Pour $a=e12a=e^{\frac{1}{2}}$ , l'équation de la tangente est

$y=f′(e12).(x−e12)+f(e12)y=f'(e^{\frac{1}{2}}) . (x-e^{\frac{1}{2}})+f(e^{\frac{1}{2}})$