Calcul de la periode
-
Ddut dernière édition par
Bonsoir c'est encore moi,
Je dois trouver la période s(t)=arcsin(t/3)
mais je ne sais pas comment procéderQuelles sont les étapes?
Merci
-
Bonsoir dut,
Quel est l'ensemble de définition de cette fonction ?
-
Ddut dernière édition par
Il y a noté dans mon cours [-1;1]
-
C'est le domaine de définition de arcsin(t).
et dans le cours pour la période ?
-
Ddut dernière édition par
je n'ai qu'un tableau avec les Df.
-
Et le graphe de la fonction ?
-
Ddut dernière édition par

-
Cette fonction est-elle périodique ?
-
Ddut dernière édition par
Pour moi oui
-
Cherche le motif qui se répète puis détermine l'intervalle sur lequel varie la variable t.
-
Ddut dernière édition par
quand je trace cette fonction je ne vois pas le motif qui se repete (hors écran)
-
Ddut dernière édition par
Le fait de ne pas voir la répétition cela signifie que la fonction n'est pas périodique?
-
Si le graphe ne montre pas de motif qui se répète, c'est que la fonction n'est pas périodique. Tu vérifies par le tableau de variations.
-
mtschoon dernière édition par

Bonjour,
Je ne fais que passer (encore une fois...)
Le graphique donné n'est absolument pas le graphique de la fonction définie par s(t)=arcsin(t/3)
Si le repère est orthonormé, il s'agit du graphique de la fonction s(t)= sin(t/3) qui effectivement est périodique (alors que la fonction arcsin ne l'est pas...)
Alors Dut, je te conseille de revoir ta question et de donner une fonction et un graphique qui correspondent.
-
Ddut dernière édition par
La question était quelle est la période de s(t)= arcsin(t/3)
Si j ai bien compris vos explication je dois coche que s(t) n'est pas périodique.période: fonction qui se répéte dans le temps comme sin ou cos ?
-
Exact.
-
Ddut dernière édition par
Merci beaucoup Noemi et Mtschoon
-
mtschoon dernière édition par

Pour information :
Graphique de la fonction s définie par $\text{s(t)=arcsin(t/3)$
fonction définie sur [-3,3], dérivable sur ]-3,3[ avec$\text{s'(t)=\frac{1}{\sqrt{1-(\frac{t}{3})^2}}\times \frac{1}{3}$
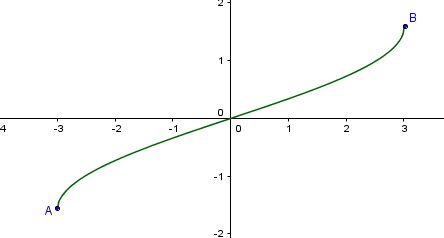
La représentation graphique est la courbe allant de A (compris) à B(compris), avec A(-3,-∏/2) et B(3,∏/2).
Fonction non périodique.
Remarque : si tu as besoin d'explication sur la périodicité d'une fonction, tu peux éventuellement regarder ici :
-
Ddut dernière édition par
Merci beaucoup Mtschoon.
Bonne soirée.
-
mtschoon dernière édition par

De rien, mais je te conseille de revoir avec soin la fonction Arcsin .