vecteurs et angles orientés

Bonjour, je demande votre aide pour cette exercice, je ne comprends pas du tout comment faire..
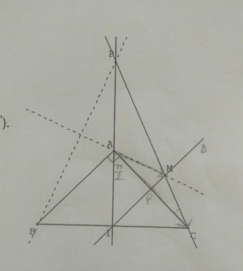
Soit ABC un triangle rectangle isocèle tel que (vecteurAB;vecteurAC)=pi/2.
Soient I le milieu de [BC] et delta la médiatrice de [AC].
Le point M est un point de delta, la droite (CM) coupe (AI) en P.

Justifier que (vecteurAM; vecteur AC) =-(vecteurCM; vecteurCA) et que (vecteurBA;vecteurBP)=-(vecteurCA;vecteurCP)
2a. Recopier et compléter :
(vecteurAM; vecteurBP)= (vecteur...;vecteurAC) +( vecteur...;vecteurBA)+(vecteur...;vecteur...)
2b. En déduire que (vecteurAM;vecteurBP)=pi/2-(vecteurCM; vecteurCP)
3a. A l'aide de la question 2, déterminer une mesure de (vecteurAM; vecteurBP)
3b. Qu'a-t-on démontré concernant les droites (AM) et (BP)?

voilà.. merci d'avance !

figure de l'exercice

Bonjour m5042849,

Utilise le fait que les triangles ACM puis PBC sont isocèles.
Utilise la relation de Chasles.

Ils sont isocèles oui mais je ne vois pas quoi en faire.

Que peut-on dire des angles MAC et ACM ?
Ecris la relation avec les vecteurs.

Ils sont égaux !

Donc
(vect AM ; vect AC) = (vect CA ; vect CM) = - (vect CM; vect CA)

D'accord merci beaucoup! Ça m'a débloqué et j'ai su faire le reste. Merci de votre aide.