Recherche d'un volume maximal

Bonjour,

J'aurai besoins d'aide pour une question, merci

Consigne: Un artisan envisage de construire, sous un hangar dont la base est un carré de vingt mètre de côté, une salle ayant la forme d'un parallélépipède rectangle. Il souhaite obtenir un volume maximal.
Il constate que son problème peut se réduire à la recherche d'un rectangle ABCD d'aire maximale, comme l'indique la figure le sommet A étant un point de la courbe représentative de la fonction f définie sur [0;10] par f(x)=2 $s q r t$ x)

Question: On note x l'abssice du point de A.
a) Prouver que l'aire (en m²) du rectangle ABCD est égale à 2(10_x) $s q r t$ x)

-ABCD est un rectangle donc Aire = Ll c'est à dire CDAD

On sait que f(x)=2 $s q r t$ x), une droite x=10 puis les droites perpendiculaires à la droite passant par A qu'on note x
⇒Donc Aire= 2(10-x) $s q r t$ x)
Mon résonnement est correct ?

b)Notons g la fonction définie sur ]0;10] par g(x)= 2(10-x) $s q r t$ x). Justifier la dérivabilité de la fonction g sur l'intervalle ]0;10] puis exprimer g'(x)
- $s q r t$ x) est dérivable sur ]0+∞[ donc dérivable sur ]0;10]

2(10-x) est dérivable sur R donc dérivable sur ]0;10]

Je suis bloquée pour exprimer g'(x)
Je sais que f(x)= $s q r t$ x) ⇒ f'(x)=1/(2 $s q r t$ x))
2 et 10 est une constante donc f'(x)=0
f(x)= x ⇒ f'(x)=1
On peut utiliser (u*v)'

Bonsoir Mllehappy,

Pour la question 1, exprime CD et AD en fonction de x

Pour la dérivée, c'est la dérivée d'un produit u x v

Pour la question 1, CD= 2 $s q r t$ x)
et AD = 10-x

Pour la question 2,
u= 2(10-x) ; u'= -1
v= $s q r t$ x) ; v'= 1/(2 $s q r t$ x)

-1* $s q r t$ x)+(2(10-x))(1/(2 $s q r t$ x)))
- $s q r t$ x) +(2(10-x))(1/(2 $s q r t$ x)))
- $s q r t$ x)+(20-2x)*(1/(2 $s q r t$ x)))

Est ce que j'ai bon, faut que je multiplie par 2 $s q r t$ x) pour mettre au même dénominateur

Attention
u' = -2

Oui, réduis au même dénominateur.

Je pense que je me suis tromper quelque part:
(-2 $s q r t$ x) * (2 $s q r t$ x)) / (2 $s q r t$ x)) + (20-2x*2 $s q r t$ x)) / (2 $s q r t$ x)) * 1/(2 $s q r t$ x))
-2 $s q r t$ x) + 20-2x * 2 $s q r t$ x)

u= 2(10-x) ; u'= -2
v= √x ; v'= 1/(2√x)

u'v + uv' = -2√x + 2(10-x)/2√x
= (-2x+10 - x)/√x
= (-3x+10)/√x

Merci,
La question suivante demande de déduire de ce qui précède les variations de la fonction g. Pour quelle valeur de x l'aire du rectangle ABCD est maximale ?

Si j'ai bien compris la question Il faut que j'étudie le signe de g'(x)
Et ensuite les variation de g.
Puis trouver l'extremun maximale grace au tableau de variation pour obtenir l'aire maximale du rectangle ABCD

Oui,
Etudie les variations de la fonction.

Donc (-3x+10)/ $s q r t$ x) = 0
-3x+10 =0
-3x=-10
x= -10/(-3)

Le signe de g' est sur [0 ; -10/(-3)[ c'est +
A -10/(-3) c'est égal à 0
Sur ]-10/(-3) ; 10] c'est -
Donc les variations de g sont croissant sur [0 ; -10/(-3)[ puis décroissant ]-10/(-3) ; 10]

Je rectifie mes erreurs:

-De signe de -3x+10.

(-3x+10)/ $s q r t$ x) = 0
-3x+10 =0
-3x=-10
x= -10/(-3)
x= 10/3

Nous travaillons sur l'intervalle ]0;10] ;
Donc dans le tableau de signe de g'(x) c'est interdit en zéro puis positif sur ]0:(10/3), ça s'annule en 10/3 et négatif sur ;10]

Ensuite on étudie les variations de g
On travaille toujours sur le même intervalle donc la valeur interdite est toujours 0 puis croissant sur ]0:(10/3) en f(10/3) puis décroissant sur ;10] en 0

Les variations sont correctes.

Pour justifier que ce soir positif puis négative c'est le signe de "a" à l'extérieur des racines ?

La valeur de x pour que l'aire du rectangle ABCD soit maximale est x=10/3

Par contre la prochaine question je ne vois pas comment procéder:
Conclure en donnant les dimensions pour lesquelles le volume de la salle est maximal, puis calculez ce volume à 1 m^3 près

Tes réponses sont correctes.

Pour les dimensions x = 10/3.

Les dimensions pour que le volume soit maximales sont :
x= 10/3 et f (10/3) ?

Il faut calculer le volume à 1m^3 près
V= Llh
V=2 $s q r t$ 10/3) * (10 - (10/3)) *
Nous avons pas la hauteur

Quelles indications donne la figure ?

Sur la correction du livre: Pour f(10/3)= (40 $s q r t$ 10)/(3 $s q r t$ 3)) mais je ne comprend pas

Ensuite pour les dimensions il on mis h = 2 $s q r t$ 10/3) ; l = 40/3 ; L = 20
Je ne comprend pas également pour la hauteur
Et je me suis tromper alors entre la Longeur et la hauteur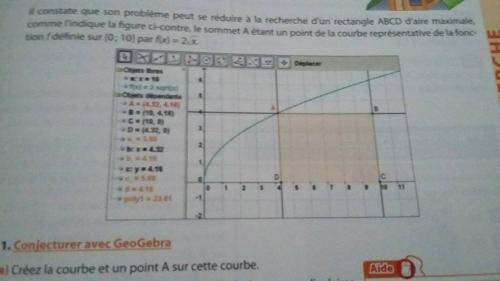

$fichier math$

La hauteur correspond à f(10/3), la longueur à celle de la pièce, pour la largeur, tu dois avoir une indication dans l'énoncé.

D'accord merci, mais je suis toujours bloquer car je n'ai pas de valeur exacte pour f(10/3)

f(10/3) = 2√(10/3)

J'ai réussi merci pour votre aide