Déterminer les coordonnées d'une droite intersection de 3 plans

[allthekpop]

Bonjour voici le point d'un exercice sur je ne comprends pas ... On le demande résoudre l'équation suivante de 3 plans :

x-y+1=0
-y+z +2=0
-x+z +1=0

On en déduit les coordonnées suivantes de la droite d qui est l'intersection des 3 plan :

X=t
Y=t+1
Z=t-1

Est ce à partir de ces équations que l'on il trouve cela ?

[mtschoon]

Bonjour,

Oui.

Les 3 équations d'inconnues x,y,z sont les équations de 3 plans.

Résoudre le système revient à trouver l'ensemble de leur(s) point(s) d'intersection.

En posantx = t( t sert de paramètre), tu trouves x, y, z en fonction de t

x-y+1=0 <=>y= x+1 <=> y=t+1

-y+z +2=0 <=> z=y-2 <=> z=.... (tu remplaces y par t+1)

-x+z +1=0 <=> z=x-1 <=> z=... ((tu remplaces x par t)

Tu trouves ainsi x,y,z en fonction de t et tu reconnais les équations paramétriques d'une droite qui est la droite d'intersection des 3 plans.

[allthekpop]

Merci beaucoup !

J'aurai d'autres questions à vous poser ...

Voici la représentation graphique du cube DIFJ

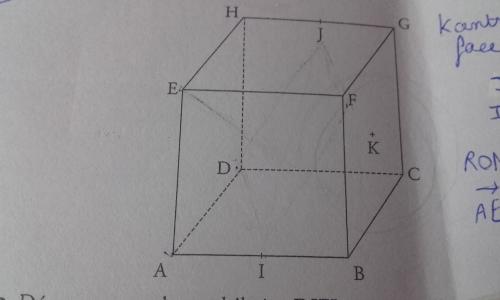
Je dois démontrer que l'aire du losange est égale à √6/2

On se place dans le RON(A,AB,AD,AE)
J est le milieu de [HG]
I est le milieu de [AB]

J'ai mis que l'aire de ce losange était DF+IJ/4 + DF+IJ/4 = DF+IF/2 mais je bloque à cet endroit ...

[mtschoon]

Merci de donner des détails sur ton énoncé.

Tu as écrit
Citation
cube DIFJDIFJ n'est pas un cube...

Citation
RONje ne sais pas ce que ça veut dire...

Citation
l'aire du losangeDe quel losange parles-tu ?

[allthekpop]

DIFJ un quadrilatère*

Repère orthonormé

Losange DIFJ

[mtschoon]

OK

Je pense que tu t'es trompé pour calculer l'aire du losange.

Pour trouver l'aire d'un losange, il faut fairele produit des diagonales et diviser par 2

$\text{aire (difj)=\frac{ij \times df}{2}$

Reposte si besoin.