Comprendre les encadrements d'intégrales
-
Aallthekpop dernière édition par Hind
Bonjour, mon baccalauréat approche et je suis en période de révision cependant je n'ai pas compris la réponse d'un exercice pouvez vous m'aider ?
On me demandait si l'affirmation de la proposition 5 était vrai ou fausse j'ai utilisée la méthode "1 carreau = 1 unité d'aire" en s'aidant du tableau de variation cependant une autre méthode est donnée mais je ne comprends pas le passage de 0≤intégrale de fx≤3 à 0≤intégrale de fx ≤4 ?
Bonne journée
-
mtschoon dernière édition par

Bonjour,
Ici, les scans de manuels ne sont pas autorisés...
J'ai dû supprimer le texte...
-
mtschoon dernière édition par

Tu pourrais faire un graphique pour comprendre les encadrements d'intégrales demandés (en prenant des rectangles - comparaison des aires). Ce serait le plus simple.
Tu peux aussi , raisonner "mathématiquement"
Je te fais le 1er cas.
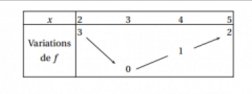
2 ≤ x ≤ 3
Avec le tableau de variation : 0 ≤ f(x) ≤ 3
donc :
$\bigint _2^3 0 dx \le\bigint_2^3 f(x)dx \le \bigint_2^3 3dx$
$0\bigint _0^3 1 dx \le\bigint_2^3 f(x)dx \le 3\bigint 1dx$
$0[x]_2^3 \le\bigint_2^3 f(x)dx \le 3[x]_2^3$
$0(3-2) \le\bigint_2^3 f(x)dx \le 3(3-2)$
Donc :
$0\le \bigint_2^3 f(x)dx \le 3$
Tu fais pareil pour le second cas ( 3 ≤ x ≤ 5 )