Programmer un algorithme qui mesure l'écart entre une courbe et sa tangente

Bonsoir,

Soit f une fonction définie et dérivable sur R , a un réel et Cf la courbe représentative de la fonction f.

a- Quelles sont les coordonnées du point Cf d'abscisse a ?
b- Quel est le coefficient directeur du point Cf d'abscisse a ?
c- Démontrer qu'une équation T est y= f'(a)x-f'(a)a+f(a).
On donne l'algorithme suivant qui mesure "l'écart" entre la courbe représentative d'une fonction f et sa tangente en un point d'abscisse a sur un intervalle.
a- Quelle est l'expression de la fonction f ?
b- Que représente F ,G et H ?
c- Combien de valeurs de S l’algorithme affiche t-il ?
a- Programmer cet algorithme (calculatrice ou algobox)
b-Faire fonctionner ce programme =0
c- Que peut on conjecturer sur la position relative de la courbe Cf représentant f et de sa tangente en O ?
d- Démontrer cette conjecture

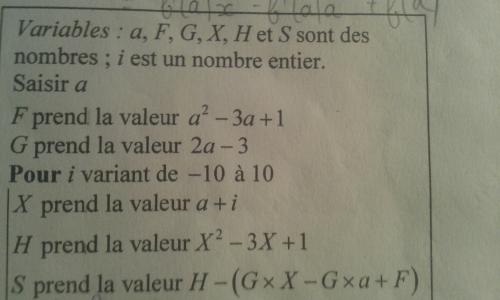
$fichier math$

les questions du 1) j'ai réussi

Concernant le 2) je vous fais part de ce que j'ai fais et de voir si cela est juste
2)a- l'expression de f est f(x)= x²-3x+1
b- F correspond à f(a) = a²-3a+1
G correspond à la dérivé de f(a)
H correspond à f(X)= X²-3X+1 avec X= a+i
c- 21 valeurs
3) a-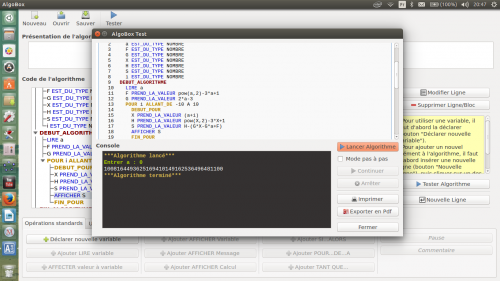 $fichier math$
la c et la d je n'y arrive pas ...

Bonsoir Anabelle2110,

Question c) Analyse l'évolution des valeurs fournies par le programme.

En ft je ne comprends le but de cet algorithme et quand a=0 cela me donne une grande valeur , je ne sais pas ce que cela veut dire...

Quels résultats obtiens tu pour i variant de -10 à 10 ?

Je suis supposée trouver 21 valeurs mais j'ai l'impression que mon algorithme n 'est pas bon

Je trouve 100,81,64,49,36,25,16,9,4,1,0,1,4,9,16,25,36,49,64,81,100

Donc quand i est négatif les valeurs obtenues diminuent et quand i est positif les valeurs augmentent

Toutes les valeurs sont positives, donc que peux t-on conjecturer sur la position de cette tangente avec a = 0 par rapport à la courbe.

Je conjecture que la courbe est au dessus de la tangente avec a=0 ?

Ensuite je dois démontrer cette conjecture ,comment dois-je m'y prendre ?

Il faut démontrer que f(x) - y ≥ 0 pour tout x.

y= f'(0)(x-1)+f(0)= -3x+1

f(x)-(-3x+1) = x²-3x+1+3x-1 = x²

Or x² est strictement croissant sur R . Donc la courbe Cf est au dessus de la tangente T avec a=0 sur R

Une erreur au début le -1 ? :

y= f'(0)(x-1)+f(0)= -3x+1
C'est
y= f'(0)(x-0)+f(0)= -3x+1

ah oui je me suis trompée merci