Fonction aire d'un rectangle

[bernard34820]

Bonsoir,

je ne sais pas comment démarrer ce satané exercice
ABC est un triangle équilatéral de côté 12cm est I est le milieu du segment AB
M est un point variable du segment AI et N le point du segment AB distinct de M tel que AM =NB
Q est le point du segment BC et P est le point du segment AC tels que MNQP soit un rectangle.

On note f la fonction qui à x=AM en cm associe l’aire du rectangle MNQP en cm2
A Quel est l’ensemble de définition de f ?
B exprimer MN puis MP en fonction de x. en deduire l’expression algebrique de f(x)
c) calculez f’3) puis vérifier que pour x de [0 ;6] :
f(x)-f(3)=-2√3(x-3)2
d) en déduire que f(3) est le maximum de f sur [0 ;6]
e) Quelles sont les dimensions du rectangle d’aire maximale ?

Merci pour votre aide
Bernard

[mtschoon]

Bonsoir,

As-tu fait un schéma ?

C'est la première chose à faire.

je t'en joins un, si besoin

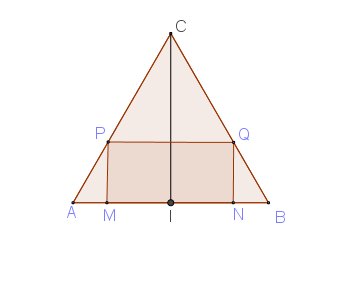
f(x)=aire(MNQP)

Le rectangle MNQP est défini pour M appartenant à [AI]

AI=6 donc 0 ≤ AM ≤ 6 c'est à dire 0 ≤ x ≤ 6

L’ensemble de définition de f est [0,6]

Essaie de poursuivre.

[bernard34820]

Bonjour,

Merci pour ta réponse,
poour la qustion b voici ce que j'ai fait
MN=2x
MP ⊥ AB
CI ⊥ AB
MP et CI ⊥ AB
AM/AD = AP/AC
AM = 3 AI = 6 AC = 12 donc
AP=12x3/6 → x/2x = AP/4x
AP= 12x3/6 → AP=4x x x / 2x
Ap = 6 →→AP = 2x
je ne sais pas déduire la valeur algébrique de f(x)
merci pour l'aide

[mtschoon]

Les réponses que tu proposes sont à revoir.

MN=AB-(AM+NB)=.............

Pour calculer MP, il y a deux voies possibles ; tout dépend de ce tu sais.

Si tu sais que tan(60°)=√3, en utilisant le triangle AMP, la réponse est immédiate

Sinon, tu peux utiliser le théorème de Thalès appliqué aux triangles.

J'ignore où est le point D dont tu parles...

$\frac{AM}{AI}=\frac{MP}{IC}$

AM=x
AI=6
(CI) est la hauteur d'un triangle équilatéral de côté 12.
Peut-être connais tu la propriété directe pour trouver CI (sinon, il faudra utiliser le théorème de Pythagore)

Vois ce qui correspond à tes connaissances.

[bernard34820]

MN=AB-(AM+NB)=6
Pythagore pour trouver CI
AC²=AI²+CI²
CI²=AC²-AI²
CI²=12²-6²
CI²=144-36
CI²=108
CI=√108
CI≈10.4
on peut donc faire
AM/AI=MP/IC
MP=3√108/6
MP=5,2

Comment a partir de ces valeurs pêut on déduire l'expression algébrique de f(x)

merci
Bernard

[Luntham]

Bonjour à tous,

M est un point variable
AB = 12 et AM = NB = x
MN= ...

[bernard34820]

MN = 6
mais comment repondre à
Comment a partir de ces valeurs pêut on déduire l'expression algébrique de f(x)

[Luntham]

Non,

MN = 12-2x

Calcule MP

[bernard34820]

Pythagore pour trouver CI
AC²=AI²+CI²
CI²=AC²-AI²
CI²=12²-6²
CI²=144-36
CI²=108
CI=√108 on peut donc faire
AM/AI=MP/IC
x/2x=MP/√108
MP=x√108/2x
est ce exact
Comment a partir de ces valeurs pêut on déduire l'expression algébrique de f(x)

[Luntham]

Il faut utiliser la valeur exacte
CI² = 108, 108 = 36 x 3
CI = 6√3

Puis si tu utilises Thales
AM/AI=MP/IC
x/6=MP/6√3
tu déduis MP = ....

Remarque : tu aurais pu utiliser directement le triangle AMP (demi triangle équilatéral) donc AP = 2AM = 2x

f(x) est l'expression de l'aire du rectangle soit MN x MP

[mtschoon]

Au final, j'espère bernard34820 que tu as trouvé :

$MP=x\sqrt{3}$

D'où

$f(x)=MN\times MP=(12-2x)(x\sqrt{3})$

Avec cela, tu dois pouvoir poursuivre ton exercice, sinon reposte.