les nombres complexes (arguments)

Bonjour ,
Déterminer et représenter l'ensemble de points M d'affixe z tel que :
a) Arg(z-2i) = -pi/4 (2pi) b) Arg(1/(z-2))= pi/3 (2pi)

pour le a) :
M ∈ E ⇔ arg(z-2i) = -pi/4 (2pi)
⇔ (vecteur u ; vecteur AM) = - pi/4 (2pi) où A(2i)
Après j'ai du mal à continuer...

Bonjour Anabelle2110,

Trace un repère, place le point A puis l'angle -π/4.
Tu déduis ensuite l'équation de la demi droite solution.

j'ai fait ce que vous m'avez dit mais je n'arrive pas à déduire l'équation ...
j'ai vraiment des difficultés avec ce genre d'exercice... :frowning2:

Bonjour,

Une piste pour le a) en attendant que Noemi soit de retour.

Tu dois fairel'interprétation géométriquede l'argument .

Soit A le point d'affixe 2i .
Dans le repère $(0,u⃗,v⃗)(0,\vec{u},\vec{v})$ orthonormé du plan complexe, tu places A de coordonnées (0,2)

$(2π)(\vec{u},\vec{am})=-\frac{\pi}{4} \ (2\pi)$

A partir du point A , tu traces un représentant du vecteur $u⃗\vec{u}$

Il te reste à placer la demi droite (Δ) d'origine A qui fait un angle de -∏/4 avec ce représentant de $u⃗\vec{u}$ .

L'ensemble des points M est cette demi-droite (Δ) construite.

Bien sûr, tu peux ensuite, en plus, déterminer l'équation de (Δ) mais je ne suis pas sûre que ça soit demandé par l'énoncé car (Δ) est parfaitement déterminée géométriquement. A toi de voir..
Si tu veux donner l'équation :
Pour x>0, (Δ) a pour équation y=ax+b
Pour trouver a et b tu peux utiliser le point A(0,2) et B(1,1) par exemple.

Reposte si l'explication n'est pas assez claire.

Dans le doute, je te joins un schéma.

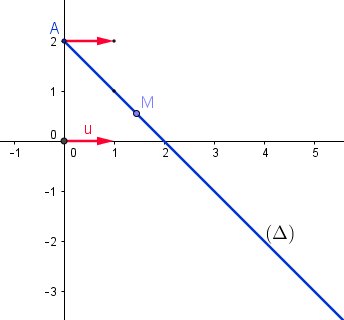
$fichier math$

Lorsque tu as compris, tu passes au b)

daccord merci ca m'aide beaucoup à comprendre

De rien !

Pour l'équation de (Δ), tu dois trouver après calculs y=-x+2 (si tu penses qu'il faut donner une équation)

Tu peux nous proposer ta réponse pour le b) si tu a besoin d'une vérification ou d'une aide.

non il n'est pas demandé de trouver l'équation de la demi-droite mais je le fais quand même et oui je trouve cela

C'est bien.
Tu passes au b) qui est du même type, après une petite transformation.

pour le b)
M ∈ E ⇔ arg(1/(z-2))= pi/3 (2pi)
⇔ arg((1-0)/(z-2) = pi/3 (2pi) où A(2) et B(0)
⇔ ( $am⃗\vec{am}$ ; $bm⃗\vec{bm}$ ) = pi/3 (2pi)

Dans le repère (0,\vec{u},\vec{v}) orthonormé du plan complexe, je place A de coordonnées (2;0) et B(0;0)
est -ce bon ce que j'ai fait ?
ensuite pour tracer la demi droite je doute...

Ta transformation du départ est à revoir

Regarde ton cours sur "argument d'un quotient".

$\fbox{arg(\frac{1}{z-2})=-arg(z-2) }$

Si ce cas particulier n'est pas écrit dans ton cours, tu peux le trouver avec le cas général :

$arg(1z−2)=arg(1)−arg(z−2)arg(\frac{1}{z-2})=arg(1)-arg(z-2)$

$(2π)arg(1)=0\ (2\pi)$ vu que 1 est un nombre réel positif (son image est sur l'axe des réels partie "réels positifs")

donc tu trouves bien $arg(1z−2)=−arg(z−2)arg(\frac{1}{z-2})=-arg(z-2)$

Ton énoncé peut s'écrire :

$(2π)-arg(z-2)=\frac{\pi}{3}\ (2\pi)$

d'où, en multipliant chaque membre de l'égalité par -1 :

$a r g (z - 2) = . . . . .$

essaie de poursuivre.*

arg(z-2) = -pi/3 (2pi)

dans le plan orthonormé je place le point A (2;0)
Puis je trace à partir du point A un représentant du vecteur u
Je trace ensuite la demi-droite d'origine A qui fait un angle de -∏/3 avec ce représentant de vecteur u.
L'ensemble des points M est cette demi-droite privée du point A

C'est bon.

et pour l'équation est ce que c est y= -7/2x + 7/4 ?

oui c'est ca il suffit de remplacer x par 2 pour vérifier et cela me donne 0
Merci de votre aide !!! :razz:
J'ai pu bien comprendre

L'équation est à revoir...

Elle est toujours de la forme y=ax+b

Tu dois utiliser le point A(2,0), mais il faut prendre un second point B qui soit vraiment sur la demi-droite. C'est là que tu as dû faire une erreur.

C'est moins "évident" que pour la question a)

Sachant que $tan(−π3)=−3tan(-\frac{\pi}{3})=-\sqrt 3$ , tu peux choisir B de coordonnées ( 3, -√3)

Après calculs, tu dois trouver pour équation y=-√3 x +2√3 (pour x > 2)

d'accord je me suis corrigée merci mais je n'aurais jamais pensé à tan(-pi/3) ...
Merci encore une fois

De rien. Tu as bien travaillé !

Remarque :
Pour le a), tu aurais pu aussi utiliser la tangente avec $tan(−π4)=−1tan(-\frac{\pi}{4})=-1$ , mais vu la simplicité, ce n'était pas indispensable d'en parler .

Ah oui