Calculs d'angles et rayon d'une sphère
-
Mmimico dernière édition par Hind
bonjour j'ai vraiment besoin de votre aide ceci est a rendre pour le 20/01/17 s'il vous plait j'ai besoin d'aide!!!
j'ai fais la 1 et 2 pour l'aire de l'hexagone j'ai trouvé 59.86cm² mais le reste je n'y parviens pas!scan de l'énoncé supprimé.
-
Bonjour mimico,
Le scan du sujet est interdit sur ce forum. (de plus il est difficilement lisible)
Recopie l'énoncé et indique tes éléments de réponse.En quelle classe es tu ?
-
Tu peux mettre le scan que de la partie du bas comprenant la forme géométrique.
-
Mmimico dernière édition par
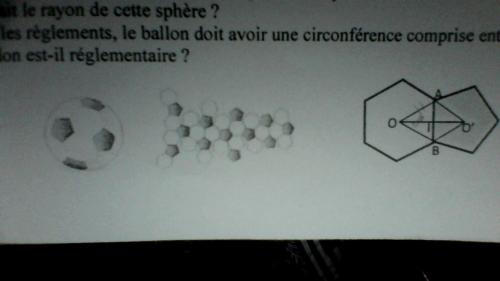
Un ballon de football n'a pas une forme sphérique: son patron est formé de 20 hexagones et 12 pentagones réguliers. Nous voulons fabriquer ce patron dont les arêtes des polygones ont pour longueurs 4.8cm. Soit O et O' les centres d'un hexagone et d'un pentagone juxtaposés par l'arrête [AB].
- Justifier que (OO') coupe [AB] perpendiculairement en son milieu I.
A cette question j'ai répondue que AOBO' est un losange et que les diagonales se coupent en leurs milieu donc OO' coupe perpendiculairement [AB].
2)Calculer l'aire de l'hexagone.
j'ai répondue A=3√3/2 ×a² où "a" exprime la longueur d'un côter donc A=3√3/2×4.8²= 59.86 cm²Et ensuite je suis bloquer pour les autres questions....
- calculer l'angle AO'I puis l'aire du pentagone
4)En déduire l'aire du patron du ballon (valeur au cm² près)
On assimile le ballon ainsi construit à une sphère de rayon r
5) Quel serait le rayon de cette sphère ?
- Justifier que (OO') coupe [AB] perpendiculairement en son milieu I.
-
Mmimico dernière édition par
Un ballon de football n'a pas une forme sphérique: son patron est formé de 20 hexagones et 12 pentagones réguliers. Nous voulons fabriquer ce patron dont les arêtes des polygones ont pour longueurs 4.8cm. Soit O et O' les centres d'un hexagone et d'un pentagone juxtaposés par l'arrête [AB].
- Justifier que (OO') coupe [AB] perpendiculairement en son milieu I.
A cette question j'ai répondue que AOBO' est un losange et que les diagonales se coupent en leurs milieu donc OO' coupe perpendiculairement [AB].
2)Calculer l'aire de l'hexagone.
j'ai répondue A=3√3/2 ×a² où "a" exprime la longueur d'un côter donc A=3√3/2×4.8²= 59.86 cm²Et ensuite je suis bloquer pour les autres questions....
- calculer l'angle AO'I puis l'aire du pentagone
4)En déduire l'aire du patron du ballon (valeur au cm² près)
On assimile le ballon ainsi construit à une sphère de rayon r
5) Quel serait le rayon de cette sphère ?
- Justifier que (OO') coupe [AB] perpendiculairement en son milieu I.
-
Mmimico dernière édition par
-
Pour la question a) comment tu justifies que le quadrilatère AOBO' est un losange ?
Pour le calcul de l'angle :
Combien y a t-il de triangles identiques dans le pentagone ?
-
Mmimico dernière édition par
Les triangles sont tous identiques puis que les arêtes mesures toutes 4.8cm
-
Les arêtes sont toutes identiques mais un triangle (OAB ou O'AB) n'est constitué que d'une arête (AB).
Quelle est la mesure de OA, O'A ?
-
Mmimico dernière édition par
et bien OA et O'A =4.8CM donc AB=9.6 non ?
-
C'est l'arête qui a pour longueur 4,8 cm donc AB = 4,8 cm.
Quelle est la mesure de l'angle AOB ?
-
Mmimico dernière édition par
bah justement je ne sais pas
-
Mmimico dernière édition par
je ne vois pas quelle démarche je pourrai utiliser pour trouver cet angle...
-
Mmimico dernière édition par
je ne vois pas quelle démarche je pourrai utiliser pour trouver cet angle...
-
Dans l'hexagone, combien peut-on tracer de triangle identique à AOB ?
De quelles natures sont ses triangles ?
-
Mmimico dernière édition par
on peut en tracer 5 et ils sont isocèles ?
-
Pour le pentagone 5 et pour
l'hexagone 6
Donc l'angle AOB a pour mesure 360/6 = .....
et
L'angle A'OB a pour mesure 360/5 = .....
-
Mmimico dernière édition par
mais sauf que moi je chercher la mesure de l'angle AO'I...
-
Tu n'as toujours pas donné la bonne réponse à la question 1.
Le triangle AOB est équilatéral et le triangle AO'B est isocèle de sommet O'.
Que peut-on dire de la forme du quadrilatère AOBO' ? puis de la droite (OO') ?
-
Mmimico dernière édition par
pour 1 c'est un losange car il a 4 cotés égaux et ses diagonales sont perpendiculaire.
Et pour le reste je comprend pas....
-
Mmimico dernière édition par
pour 1 c'est un losange car il a 4 cotés égaux et ses diagonales sont perpendiculaire.
Et pour le reste je comprend pas....
-
L'aire du triangle AO'B est inférieure à l'aire du triangle AOB. C'est une structure "cerf volant"
Pour l'angle le triangle AO'B est isocèle en O', avec l'angle AO'B = 360/5 = 72°,
(O'I) est hauteur mais aussi bissectrice donc l'angle AO'I = 72/2 = ....
-
Mmimico dernière édition par
donc AO'I=36° ?
Ensuite je sais que pour l'aire du pentagone la formule c'est 5×(base×hauteur÷2)
mais je n'est pas IO' pour la hauteur...
-
Utilise la trigonométrie.
-
Mmimico dernière édition par
je t'avoue que j'ai pas eu de prof de maths en 3eme donc sa me parait compliquer .... Il n'y a pas une autre méthode ?
-
Non,
Les données sont pour le triangle rectangle AIO', la mesure de AI = 2,4 cm et l'angle AO'I = 36°
tu utilises tan AO'I = AI/IO' et tu en déduis IO'
IO' = .....
-
Mmimico dernière édition par
Mais l'angle AO'I n'est pas égal a 36° ?
-
Oui 36°