fonction logarithme et exponentielle
-
Ssophie90 dernière édition par
Bonjour,
j 'ai fais l'exercice n°5 d 'entrainement du fichier.la dernière question me pose problème ,je ne l'a comprends pas.
voici les resultats est ce juste svp?f(x)=ln(1+ex)f\left( x \right) =ln\left( 1+{ e }^{ x } \right)f(x)=ln(1+ex)
Q1:limites
limx→∞ln(1+ex)=limx→∞lnex+ln(1+e−x)=limx→∞x+ln(1+e−x)=limx→∞x\lim _{ x\rightarrow \infty } \quad ln\left( 1+{ e }^{ x } \right) =\lim _{ x\rightarrow \infty } \quad ln{ e }^{ x }+ln\left( 1+{ e }^{ -x } \right) =\lim _{ x\rightarrow \infty } \quad x+ln\left( 1+{ e }^{ -x } \right) =\lim _{ x\rightarrow \infty } \quad xlimx→∞ln(1+ex)=limx→∞lnex+ln(1+e−x)=limx→∞x+ln(1+e−x)=limx→∞x
$\lim _{ x\rightarrow \infty } \quad ln\left( 1+{ e }^{ x } \right) =\infty \$
limx→−∞ln(1+ex)=limx→−∞ln(1+0)=0\lim _{ x\rightarrow -\infty } \quad ln\left( 1+{ e }^{ x } \right) =\lim _{ x\rightarrow -\infty } ln(1+0)=0limx→−∞ln(1+ex)=limx→−∞ln(1+0)=0Q2 signe de fff et variations
$1+{ e }^{ x }>1\quad, \quad ln\left( 1+{ e }^{ x } \right) >ln1$$\quad ,\quad\forall x\in{\displaystyle \mathbb {r} }, f\left( x \right) >0$
f′(x)=exex+1,f'\left( x \right) =\frac { { e }^{ x } }{ { e }^{ x }+1 },f′(x)=ex+1ex, , ${ e }^{ x }+1>{ e }^{ x }$
$1>\frac { { e }^{ x } }{ { e }^{ x }+1 } >0$ ,
$1>f'\left( x \right) >0$
f′f'f′ est bornée par des valeurs positives!
$\quad ,\quad\forall x\in{\displaystyle \mathbb {r} }, f'\left( x \right) >0$ alors fff est strictement croissante et en plus positive.
Q3
x+ln(1+e−x)=x+ln(1+exex)=x−xlne+ln(1+ex)=ln(1+ex)x+ln\left( 1+{ e }^{ -x } \right) =x+ln\left( \frac { 1+{ e }^{ x } }{ { e }^{ x } } \right) =x-xlne+ln\left( 1+{ e }^{ x } \right) =ln\left( 1+{ e }^{ x } \right)x+ln(1+e−x)=x+ln(ex1+ex)=x−xlne+ln(1+ex)=ln(1+ex)
$\leftrightarrow \$,∀x∈r,\quad ,\quad\forall x\in{\displaystyle \mathbb {r} },,∀x∈r,x+f(−x)=f(x)x+f\left( -x \right) =f\left( x \right)x+f(−x)=f(x) l'egalité est vérifié!
dans Q1 ,f(x)f\left( x \right)f(x) ∼\sim∼x en+∞\infty∞
le calcul$f\left( x \right) \$−f(−x)- f\left( -x \right)−f(−x) après simplification me donne xxxmais je ne comprends pas le sens de cette Question!
Merci, d avance.
-
mtschoon dernière édition par

Bonjour,
Pour Q1 et Q2, tu as bien marqué l'énoncé
Pour Q1 : limites
Pour Q2 : signe de variations de ftes réponses sont correctes
Mais, pour Q3 : il faudrait que tu marques l'énoncé (la question n'est pas écrite...)
-
Ssophie90 dernière édition par
Bonjour,mtschoon
Demontrer:
,∀x∈r,\quad ,\quad\forall x\in{\displaystyle \mathbb {r} },,∀x∈r,x+f(−x)=f(x)x+f\left( -x \right) =f\left( x \right)x+f(−x)=f(x)
en deduire que la courbe C admet en+∞+\infty+∞ une asymptote noté △\triangle△ ,préciser la position de la courbe C par rapport a △\triangle△*C courbe defff
merci
-
mtschoon dernière édition par

Il faut que tu utilises la définition d'asymptote oblique ( en espérant qu'elle est dans ton cours...)
Si f(x)=ax+b+ϕ(x) avec limx→+∞ϕ(x)=0f(x)=ax+b+\phi(x) \ avec\ \lim_{x\to +\infty}\phi(x)=0f(x)=ax+b+ϕ(x) avec limx→+∞ϕ(x)=0,
alors la droite (Δ) d'équation y=ax+b est asymptote à la représentation graphique de f, en +∞
( définition identique lorsque x tend vers -∞ )
Ici, f(x)=x+f(−x)f(x)=x+f(-x)f(x)=x+f(−x)
f(−x)=ln(1+e−x)f(-x)=ln(1+e^{-x})f(−x)=ln(1+e−x)
Tu prouves facilement que limx→+∞f(−x)=0\lim_{x\to +\infty}f(-x)=0limx→+∞f(−x)=0
Doncla droite (Δ) d'équation y=x est asymptote à la représentation graphique de f en +∞
Ensuite, tu prouves que pour tout x réel f(-x) > 0 doncla représentation graphique de f est au-dessus de (Δ)
-
mtschoon dernière édition par

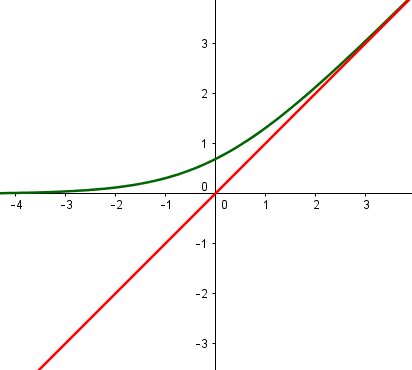
Illustration graphique
-
Ssophie90 dernière édition par
mtschoon,
je comprends mieux maintenant cette histoire de droite oblique et effectivement je savais que ce n 'étais plus d'actualité en S.Le prof me l'avais dis en début d'année.Je viens de finir de bosser sur ce type d'asymptote ,
Est ce que mon raisonnement est correct?
je suppose que ∃△\exists\triangle∃△: tels que y=ax+by=ax+by=ax+b
On a:
x+ln(1+e−x)x+ln\left( 1+{ e }^{ -x } \right)x+ln(1+e−x)=f(x)f(x)f(x)a=limx→∞f(x)x=limx→∞x+ln(1+e−x)x=limx→∞1+ln(1+e−x)x=1a=\lim _{ x\rightarrow \infty } \frac { f\left( x \right) }{ x } =\lim _{ x\rightarrow \infty } \frac { x+ln\left( 1+{ e }^{ -x } \right) }{ x } =\lim _{ x\rightarrow \infty } 1+\frac { ln\left( 1+{ e }^{ -x } \right) }{ x } =1a=limx→∞xf(x)=limx→∞xx+ln(1+e−x)=limx→∞1+xln(1+e−x)=1
a=1a=1a=1
limx→∞(f(x)−x)=limx→∞(f(−x)+x−x)=limx→∞f(−x)=b\lim _{ x\rightarrow \infty } \left( f\left( x \right) -x \right) =\lim _{ x\rightarrow \infty } \left( f\left( -x \right) +x-x \right) =\lim _{ x\rightarrow \infty } f\left( -x \right) =blimx→∞(f(x)−x)=limx→∞(f(−x)+x−x)=limx→∞f(−x)=b
or limx→∞f(−x)=0\lim _{ x\rightarrow \infty } f\left( -x \right)=0limx→∞f(−x)=0,b=0b=0b=0
On a montré que: ∃△\exists\triangle∃△: tels que y=xy=xy=x asymptote oblique!
$f\left( x \right) >x,\quad \leftrightarrow \quad \quad f\left( -x \right) >0$
$\leftrightarrow 1+\frac { 1 }{ { e }^{ x } } >1$
$\leftrightarrow \quad ln\left( 1+{ e }^{ -x } \right) >ln1$
$\leftrightarrow \quad \quad \quad f\left( -x \right) >0$
On a montré que$f\left( x \right) >x$
Cl: la courbeC est au dessus de l'asymptote!
Le graphique conforte le résultat obtenu.
Merci mtschoon,
-
mtschoon dernière édition par

C'est bon.
Ta démarche ( trouver a et b ) est exacte (si tu la connais, mais je ne suis pas sûre qu'elle soit encore au programme de TS...)
Evidemment, elle n'était pas nécessaire vu que l'asymptote devait se déduire directement de f(x)=x+f(-x)
-
Ssophie90 dernière édition par
Oui vous avez raison ce n est plus au programme de TS,
J ai vu cette méthode dans un livre et je l'ai appliquée au problème.De toute façon faut toujours aller en profondeur pour éviter d'être largué l'année prochaine.Merci,pour la fiche.
-
mtschoon dernière édition par

Oui, des notions d'analyse de TS sont passées en PostBac mais les connaître ne peut pas faire de mal.
Bon travail !