Montrer l'existence de la fonction réciproque
-
Ssophie90 dernière édition par Hind
Bonjour,
pour un exercice de niv TS +je cherche a montrer de façon rigoureuse qu'une fonction est bijective ou pas
Mon idée,
1)je sais quef(x)f(x)f(x) admet plusieurs antécédent suriii, donc non bijective..Par le calcul algèbrique,f(x)=mf(x)= mf(x)=m avec m∈m\inm∈${\displaystyle \mathbb {r} } \$
On résoud cette intersection et on déduis ttes les solutions,,Par le calcul littéral?
j 'ai supposéfff non bijective
a,a′∈ia, a'\in ia,a′∈i...
Est ce la bonne démarche?2)Jai lue pas mal de chose aussi sur les fonctions réciproques, étroitement liées à la bijection.
pourfff bijective.
-je démontre l'existence de la fonction réciproque?
merci
-
Bonjour sophie90,
Un lien vers un cours :
http://www.ai.univ-paris8.fr/~audibert/ens/07-APPLICATIONS.pdf
-
mtschoon dernière édition par

Bonjour,
Pour parler de bijection, il faut préciser l'ensemble de départ et l'ensemble d'arrivée.
f bijective de I vers J signifie que tout élément de I a une image (unique) , par f, dans J, et que tout élément de J a un antécédent (unique), par f, dans I.
Si tu parles de fonction numérique à variable réelle définie par sa formule explicite, il te suffit d'utiliser la continuité et le sens de variation.
Toute fonction f continue et strictement monotone de I vers J est bijective de I vers J.
Tu peux alors définir sa bijection réciproque f−1f^{-1}f−1 de J vers I
-
mtschoon dernière édition par

Je te donne un exemple
f(x)=x−1f(x)=\sqrt{x-1}f(x)=x−1
Soit I=Df=[1,+∞[
En étudiant les variations de f, tu peux justifier que f est bijective de I=[1,+∞[ vers J=[0,+∞[
(fonction dérivable, donc continue, et strictement croissante de [1,+∞[ vers [0,+∞[)Tu peux alors définir f−1f^{-1}f−1 bijection de J=[0,+∞[ ver I=[1,+∞[
Soir x appartenant à J=[0,+∞[
f−1f^{-1}f−1(x)=y <=> x=f(y) <=>x=y−1x=\sqrt{y-1}x=y−1
Par élévation au carré ( car x appartient à [0,+∞[ ) :
x²=y-1 <=> y=x²+1
Conclusion
f−1(x)=x2−1f^{-1}(x)=x^2-1f−1(x)=x2−1 pour x∈[0,+∞[x\in [0,+\infty[x∈[0,+∞[
Bonnes réflexions !
-
Ssophie90 dernière édition par
Merci, pour la fiche noemi, sa m'aidera tôt ou tard,
mtschoon,
je comprends mieux,c'est très claire.
j ai appliqué vôtre raisonnement à f(x)=x2f(x)=x^2f(x)=x2fonction polynôme ,définie et dérivable sur son ensemble de définition.
on a
f:f:f:r↦r+\mathbb {r} \mapsto \displaystyle \mathbb {r+}r↦r+.On peut dans ce cas prècis directement conclure quefff est non bijective car non monotone sur dfdfdf. On posex2x^2x2=a=a=a d'oux=±ax=\pm\sqrt { a }x=±asi
f:f:f:r+↦r+\mathbb {r+} \mapsto \displaystyle \mathbb {r+}r+↦r+ strictement croissante donc monotone surdfdfdfOn a l'unicité de la solution.
C'est une bijection.
il existe alors une fonction reciproque,f−1(x)=x{ f }^{ -1 }(x)=\sqrt { x }f−1(x)=x définie sur r+↦r+\mathbb {r+} \mapsto \displaystyle \mathbb {r+}r+↦r+On a du restreindre l'etude pour faire apparaître la bijection de $f \$
merci,
-
mtschoon dernière édition par

C'est bon ! Tu sembles avoir bien maîtrisé.
Un petit détail : pour la bijection, parle de fonction" strictement monotone" (pas seulement monotone)
Un complément éventuel :
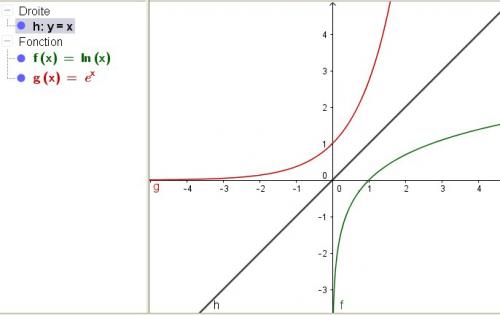
En repère orthonormé, f et f−1f^{-1}f−1 ont leurs représentations graphiques symétriques par rapport à la droite d'équation y=x, ce qui est logique.
Le plus bel exemple que tu peux trouver comme bijections réciproques l'une de l'autre dans ton programme de TS est le cas des fonctions logarithme et exponentielle.
-
Ssophie90 dernière édition par
Bonjour,
ah oui super on vois bien que les courbes sont toutes les deux symétrique par rapport a xxx .je posterai demain l'exercice sur ce sujet,
merci,
-
mtschoon dernière édition par

D'accord.