fonction dérivée et étude des variations d'une fonction
-
Cchacha8 dernière édition par
Bonsoir,
J'ai un devoir a rendre
Pourriez vous m'aidez svp
je vous es mis en PJ le documentMerci à vous
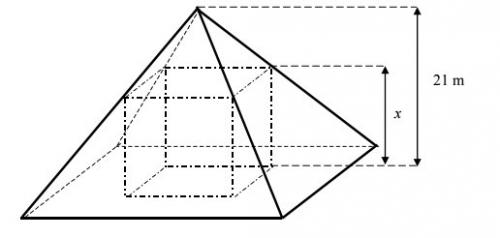
Scan du gaphique effectué par mtschoon
merci d'écrire l'énoncé à la main.
-
Cchacha8 dernière édition par
Bonsoir Désolé je ne savais pas
On considère une pyramide de hauteur 21 m
On veut construire, à l’intérieur de cette pyramide, une salle ayant la forme d’un
parallélépipède rectangle ; soit x, exprimé en mètres, la hauteur de cette salle.
Problématique : On veut connaître la hauteur x pour laquelle le volume V de cette salle est
maximal.Le volume V de cette salle, exprimé en m3, est donné par la formule :
V(x)=25/9(x^3-42x^2+441x)-
Donner l’intervalle dans lequel se situent les valeurs de x.
-
Compléter les valeurs en donnant les volumes lorsque x vaut 3, 15 et 21.
-
Les questions 1 et 2 permettent-elle de déduire pour quelle valeur de x le volume de la salle
est maximal ? Proposer une méthode permettant d’accéder à cette valeur
On étudie la fonction f définie sur [0 ; 21] par : f x = 25/9 ( x^3 - 42x^2 + 441x)
-
À l’aide de la calculatrice, tracer la courbe représentative de la fonction f sur [0 ; 21].
-
À partir du graphique précédent, donner une estimation de la valeur de x correspondant au
volume maximal. -
Calculer f ’(x).
-
a) Résoudre f ’(x) = 0.
b) Vérifier les solutions à l’aide d’un programme de la calculatrice. Préciser si les résultats
affichés sont cohérents avec ceux de la question précédente.- En déduire la hauteur x pour laquelle le volume V est maximal et donner la valeur de ce
volume.
Merci
-
-
mtschoon dernière édition par

Bonjour,
Piste pour démarrer,
-
Comprends le schéma et l'énoncé. Tu dois trouver 0 ≤ x ≤ 21
-
Pour trouver V(3), dans V(x) tu remplaces x par 3 et tu comptes.
Idem Pour V(15) et V(21)
-
-
mtschoon dernière édition par Casebas

Je viens de constater que ce sujet a été partiellement traité ici, il y a pas mal de temps...
Regarde si cela peut t'être utile.
Reposte si besoin.
Bon travail.