Montrer qu'une suite est géométrique et donner son expression

[jen78]

Bonjour j'aurais aimé avoir des explications car il y a certaines questions où je n'y arrive pas

Dans cet exercice on considère la suite (Un) définie par u0=3 et Un+1= 2-Un/Un

On pose également Vn= Un-1/Un+2

1. Calculer U1 et U2

2. Exprimer Vn+1 en fonction de Vn

3. Montrer que (Vn) est une suite géométrique. Donner son premier terme et sa raison

4. Exprimer Vn en fonction de n pour tout n appartenant à N

5. Exprimer Un en fonction de Vn pour tout n appartenant à N

6. En déduire, pour tout n appartenant à N, l’expression de Un en fonction de n

7. Conjecturer la limite l de Un

8. Ecrire un algorithme permettant de trouver la plus petite valeur de n pour laquelle |Un-l| <0.1

Voici ce que j'ai fais:

1. U1= -1/3 U2= -7

2. Je trouve -2Vn

3. Je trouve q= -2 et donc -2Vn ( elle est bien géométrique)

4.Vn= 2/5* (-2)^n

5. (2Vn+1)/(1-Vn) or je n'arrive pas à factorisé, je sais que c'est par -1 mais je n'y arrive pas

6. Je sais que Un= U0 + nr mais je ne trouve pas la raison

7;8. Je n'arrive pas à ces questions

J'aimerais simplement des explications pour mieux comprendre et ainsi mieux réussir, merci d'avance !

[mtschoon]

Bonjour,

Une remarque sur l'écriture

Je suppose qu'il faut comprendre
$u_{n+1}=\frac{2-u_n}{u_n}$ et $v_n=\frac{u_n-1}{u_n+2}$

Si tu n'utilises pas les codes Latex, pour éviter toute ambiguité, mets suffisamment de parenthèses et écris :

$<strong>U$_{n+1}$=(2-U$_n$)/U_n$ et**$V$_n$=(U$_n$-1)/(U_n$+2)**

Je regarde tes réponses

1) et 2) : c'est bon

3) c'est bon mais vu la question, il faut préciser que le premier terme vaut 2/5

4) et 5) : c'est bon

Pour le 5), je ne vois pas l'intérêt de mettre -1 en facteur...
Si tu veux vraiment le faire, tu mets (-1) en facteur en changeant les signes ou bien du numérateur ou bien du dénominateur ( mais pas les deux ! )

6) : ta proposition est fausse car (Un) n'est pas une suite arithmétique.
(Un) est une suite quelconque, ni arithmétique, ni géométrique.

Tu sais que $u_n=\frac{2v_n+1}{1-v_n}$

Dans cette écriture, tu remplaces Vn par ce que tu as trouvé, c'est à dire $\frac{2}{5}(-2{)}^n$

Pour la 7), on te demande seulement une conjecture.
Suivant ce que tu connais, tu as plusieurs méthodes possibles.

Il y a une méthode graphique, si tu l'as vu en cours.

Tu peux aussi, prendre un logiciel (ou ta calculette) qui te calcule les valeurs de Un
Par exemple, voici une réponse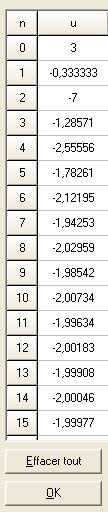

Tu peux constater que les termes s'approchent de -2 (en oscillant autour de -2) d'où la conjecturel=-2

Tu peux bien sûr faire une démonstration rigoureuse (c'est mieux, mais ce n'est pas demandé)

Pistes :

$u_n=\frac{2v_n+1}{1-v_n}$

Tu mets Vn en facteur au numérateur et au dénominateur puis tu simplifies par Vn

Tu dois obtenir

$u_n=\frac{2+\frac{1}{v_n}}{\frac{1}{v_n}-1}$

Lorsque n tend vers +∞, Vn tend vers +∞ ou -∞ suivant la parité de n, donc $\frac{1}{v_n}$ tend vers 0

La limite de $u_n$ est donc$\frac{2}{-1}$, c'est à dire $-2$

$\boxed{l=-2}$

Regarde tout ça de près.

[mtschoon]

Je te joins un programme fait avec AlgoBox pour répondre à ta dernière question.

La plus petite valeur de n pour laquelle |Un-l| < 0.1 et 7

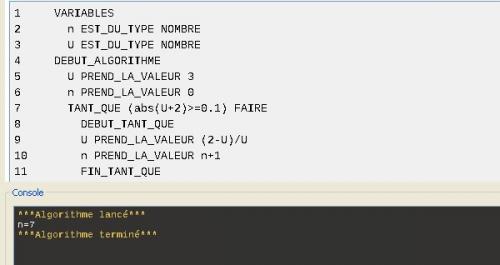
Regarde le programme et adapte le à tes habitudes de programmation.