DM triangle de Von Koch

bonjour,
on considère la construction du triangle de Vonkoch.
on part d'un triangle équilatéral de côté 1 ce qui constitue le flocon f1.
on note Cn le nombre de côté d'un flocon, Ln la longueur d'un segment du flocon et Pn le périmètre du flocon.
ainsi, C1=3, L1=1 et P1=3
Pour le flocon f2, C2=12, L2= 1/3, P2=4 (12*0.5)
Dans la construction du segment, chaque côté est divisé en 3, on garde deux morceaux et on en rajoute deux.
Le nombre de côté est donc multiplié par 4 à chaque étape. Ainsi, Cn+1=4Cn (suite géométrique), on a aussi Ln+1=1/3Ln (suite géométrique)
ainsi, on prouve que le périmètre est infini.

calculer l'aire exacte de F1
on note Sn l'aire de Fn , montrer que Sn+1=Sn+(4/9 puissance n-1* racine de 3/12
montrer que si on a a=b+alpha u
b=c+alpha v
c=d+alpha w
alors a=d+alpha (u+v+w)
en vous aidant de la question 2 et 3, démontrer que le flocon a pour limite une aire de 2 racine de 3 /5

Bonjour,

Le triangle de Von Koch (en deux mots) est un classique.

Tu peux trouver des indications un peu partout sur le web.

Eventuellement, je te mets un lien ( regarde l'exercice 1 , étude relative à l'aire)

http://www.lyc-rostand-mantes.ac-versailles.fr/IMG/pdf/1S-DM5-C-3.pdf

Reposte si besoin.

Bonjour,

Le flocon de Von Koch est effectivement un classique des figures fractales.
Il est construit itérativement en partant d'un triangle équilatéral sur lequel à chaque étape, on rajoute de nouveaux triangles équilatéraux.

Pour le point 1) il faut simplement commencer par appliquer la formule de l'aire d'un triangle équilatéral de côté 1.
La formule de l'aire d'un triangle étant $base \times hauteur / 2$ , tu peux trouver la hauteur de ce triangle en appliquant le théorème de pythagore.
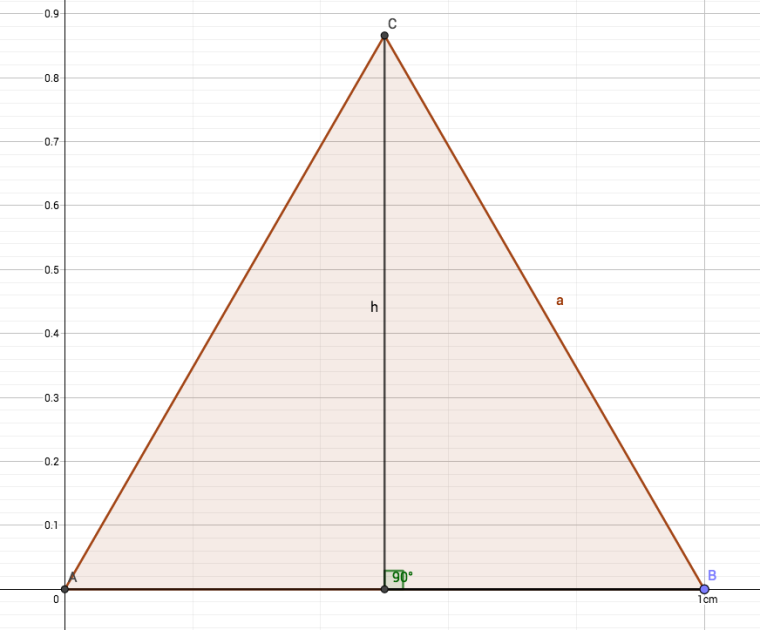
0_1513436716116_Capture d’écran 2017-12-16 à 16.04.53.png

merci, ça m'a bien aidé pour les deux premières questions, mais je suis bloqué à la question 3 et 4 et je ne trouve rien sur internet... Pouvez-vous m'aider svp???

@cedren

Je t'explique pour la question 3)

$a=b+αua=b+\alpha u$
$b=c+αvb=c+\alpha v$
$c=d+αwc=d+\alpha w$

En ajoutant membre à membre, tu obtiens

$a+b+c=b+c+d+αu+αv+αwa+b+c=b+c+d+\alpha u+\alpha v+\alpha w$

En factorisant une partie du membre de droite

$a+b+c=b+c+d+α(u+v+w)a+b+c=b+c+d+\alpha (u+ v+ w)$

En simplifiant par b+c

$d+\alpha (u+ v+ w)$

CQFD

Essaie de faire la 4), sinon reposte.

merci beaucoup, pour la 4), je dois prouver que la limite de Sn lorsque n tend vers l'infini est 2 racine de 3/5, j'ai trouver sur le lien que m'avez m'avez envoyer un exercice correspondant à ça ou l'on trouve bien que la limite est 2 racine de 3/5 ou la résolution commence par "puisque 4/9 est comprise entre -1 e 1", mais à quoi correspond ce 4/9?

Tu n'as pas besoin de lien et je ne sais pas trop où tu bloques.

Essaie de faire une démarche logique, comme te le demande ton énoncé, pour exprimer $S_n$ et déterminer sa limite.

Si tu as fait la question 2) comme tu l'as indiqué précédemment, tu as démontré que :
$\fbox{S_{n+1}=S_n+(\frac{4}{9})^{n-1}\frac{\sqrt 3}{12}}$

L'idée est d'utiliser la méthode vue à la 3) avec a,b,c,d à $S_n , S_{n-1}, ...S_2,S_1$

Tu peux écrire :
$Sn=Sn−1+(49)n−2312S_{n}=S_{n-1}+(\frac{4}{9})^{n-2}\frac{\sqrt 3}{12}$
$Sn−1=Sn−2+(49)n−3312S_{n-1}=S_{n-2}+(\frac{4}{9})^{n-3}\frac{\sqrt 3}{12}$
...
...
$S3=S2+(49)1312S_{3}=S_2+(\frac{4}{9})^{1}\frac{\sqrt 3}{12}$
$S2=S1+(49)0312S_{2}=S_1+(\frac{4}{9})^{0}\frac{\sqrt 3}{12}$

En utilisant la méthode du 3), tu obtient

$Sn=S1+312[(49)0+(49)1+...+(49)n−3+(49)n−2]S_n=S_1+\frac{\sqrt 3}{12}[(\frac{4}{9})^{0}+(\frac{4}{9})^{1}+...+(\frac{4}{9})^{n-3}+(\frac{4}{9})^{n-2}]$

La quantité entre crochets est la somme de termes d'une suite géométrique . Tu explicites cette somme.
Ensuite, tu prendras la limite de cette expression trouvée pour $S_n$

d'accord, mais quelle est la quantité entre crochets? comment je la calcule?

@mtschoon

Tu utilises la formule de la somme relative aux suites géométriques.
Le premier terme est $(49)0=1(\frac{4}{9})^0=1$
La raison est $49\frac{4}{9}$
Le nombre de termes est (n-1)

ça me donne comme résultat 1.8-4.05*(0.444444)n
comment je peux calculer la limite de cette expression?

D'abord, écris l'expression de $S_n$ de façon exacte , non avec des valeurs décimales approchées.

Pour la quantité entre crochets, tu dois obtenir:

$1×1−(49)n−11−491\times \frac{1-(\frac{4}{9})^{n-1}}{1-\frac{4}{9}}$

A simplifier, bien sûr

Ensuite, pour la limite, regarde ton cours sur les suites géométriques, avec la raison comprise entre 0 et 1:

la limite de $(49)n(\frac{4}{9})^n$ , lorsque n tend vers $+∞+\infty$ est 0

Je pense que tu as maintenant tous les éléments utiles pour terminer ton exercice.