Fonction Exponentionnelle et Intégrale

Bonsoir

je ne comprends pas cet exo
pouvez vous m aider
merci à vous

(énoncé scanné supprimé)

Bonsoir Tourtois62,

Les scans d'énoncés ne sont pas autorisés.

Merci de taper l'énoncé et d'indiquer les questions qui te posent problème.

bonjour

Désolé mais comme je ne savais pas comment recopier le début de l'énoncé j'avais préféré les scanner

donc la fonction f définie sur R par $e^{-\frac{x^2}{2}}$ et I sa courbe représentative dans le repère

Pour tout réel on pose Intégrale $∫0ae−x22dx\displaystyle \int _0^a e^{-\frac{x^2}{2}}dx$

1- etudier le sens de variation de f sur R

Donc j'ai fait f(x) = e^(-x^2/2)
f'(x) = 2*(-2x)/2^2*e^(-x^2/2)
= -4x/4e^(-x^2/2)=-xe^(-x^2/2)

tableau
x - infini 0 + infini
f'(x) + -

2- déterminer la limite de f en + infini interpreter graphiquement ce résultat
j'ai fait lim (-x^2/2)= - infini
lim e^(-x^2/2) = 0
asymptote horizontale y = 0

3- justifier que I(a) existe et interpréter graphiquement cette intégrale pour a positif

je ne comprends pas du tout la 3ème question
pourriez vous me dire si c'est correct pour les 2 premières

merci à vous

Effectivement, sans LaTex, c'est dur à écrire et à lire...

Pour la 1)

Même si ce n'est pas demandé tu peux préciser que la fonction f est paire (donc symétrie de la courbe par rapport à l'axe des ordonnées).

Je pense que tu as compliqué pour calculer f'(x), mais le résultat est bon .
La dérivée de $e^{u(x)}$ est $eu(x)×u′(x)e^{u(x)}\times u'(x)$
$f′(x)=e−x22(−x)f'(x)=e^{-\frac{x^2}{2}}(-x)$

La tableau de variation de f est bon mais précise le maximum pour f :
pour $x = 0, f (x) = 1$

Pour la 2), c'est bon.

Pour la 3), il te suffit d'appliquer ton cours car tu n'as aucun calcul à faire (la valeur de I(a) n'est pas demandée),

On te demande seulement une explication.

Piste pour l'explication :
f est définie, dérivable donc continue sur R donc intégrable sur tout intervalle de R , en particulier sur les intervalles de bornes 0 et a (a réel), donc I(a) existe.

Pour a positif, I(a) représente l'aire de la portion du plan limitée par l'axe des abscisses, la courbe représentative de f, la droite d'équation x=0 (axe des ordonnées) et la droite d'équation x=a.

Je te conseille de faire la représentation graphique de f, de placer a ( a positif) et de hachurer la portion du plan concernée, pour éclairer ton explication.

Bonsoir et merci à vous

désolé mais je bloque vraiment sur la 3ème question

@tourtois62
La 3ème question est :" justifier que I(a) existe et interpréter graphiquement cette intégrale pour a positif "

Je t'ai déjà répondu ...
Regarde ton cours sur la définition d'une intégrale car je pense que c'est là ton problème.
Relis ma réponse précédente avec soin et indique ce que tu ne comprends pas sur I(a).

Si ça peut t'aider, je te joins un graphique

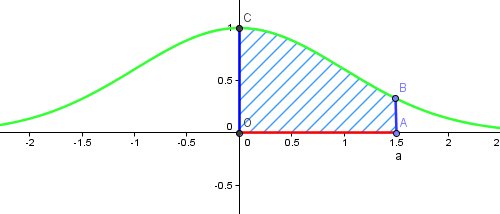
Sur le schéma, j'ai pris a =1.5

Interpétation graphique de I(a) : I(a) est l'aide de la zone hachurée, l'unité d'aire étant l'aire du carré (ou rectangle) construit sur les vecteurs unitaires de chaque axe.

Comme déjà indiqué, c'est tout ce que tu as à faire car la valeur de I(a) n'est pas demandée.

Bon travail !

Merci à vous pour votre aide

De rien !
Si tu as assimilé cette notion d'intégrale, c'est parfait !

Bonjour

je dois trouver la primitive de e^(-X^2/2)

je ne sais pas comment

Salut

Une primitive de f(x) = e^(-x²/2) ne peut pas être exprimée par un nombre fini de fonctions élémentaires.

On me demande d exprimer l'aire à l'aide d une intégrale

Une primitive de $e−x22e^{-\frac{x^2}{2}}$ ne peut pas s'exprimer avec une fonction usuelle.
On ne peut pas te poser cette question.

Pour exprimer l'aire à l'aide d'une intégrale, s'il s'agit toujours de la question 3), c'est déjà fait

L'aire hachurée sur le graphique que je t'ai donné précédemment vaut $∫0ae−x22dx\displaystyle\int_0^a e^{-\frac{x^2}{2}}dx$

non c'est un autre question

sur un autre dessin qui ressemble au votre
on me demande d'exprimer son aire à l'aide d une intégrale enfin justifier que cette aire est égale à I(1) en ua

S'il s'agit du même exercice et de la même fonction, il faudrait que tu donnes le dessin (les scans de dessins sans texte sont autorisés) et la question précise.
Je pense que, tout simplement, cette fois a=1, le point A de mon schéma a pour coordonnées (1,0) et B (1, f(1) ) .
Ainsi le nouveau quadrilatère curviligne (OABC) a une aire qui vaut
$∫01e−x22dx=I(1)\displaystyle\int_0^1 e^{-\frac{x^2}{2}}dx =I(1)$