algorithme : somme des carrés des chiffres d'un nombre entier

bonsoir j'espère que qlq un m'aidera à résoudre cet algo ; je l'ai déja étudié ça fait un an mais j'ai tout oublié alors que je l'aurai dans le concours merci d'avance
écrire en pseudo langage; l'algorithme qui calcule la somme des carrés des chiffres d'un nombre entier n
on suppose que vous disposez des fonctions quotient (a;b) et reste (a;b) qui calculent et retournent respectivement le quotient et le reste de la division euclidienne de l'entier a par l'entier b (b*0) j'ai fait un essai
variable a;b;c;A;B;C;S : entier
ecrire("entrez le chiffre");
lire(abc);
A----a * a
B-----b * b
S----A+B
Ecrire ( "la somme="; S)

Bonjour hiba

Une piste
tu utilises,comme indiqué, la division euclidienne en prenant 10 comme diviseur
a = 10 q + r
tu sommes le carré du reste S = $r^2$
tu choisis le quotient comme nouveau nombre et tu réitères le même raisonnement;
q = 10q' + r'
S = S + $r'^2$
fin du calcul des que le quotient est nul.

@noemi
variable a; q;S : entier
ecrire(entrez le chiffre);
lire(a);
ecrire(entrez un diviseur);
lire(d)
a----a div d+a mod d
S---- a mod d *2
ecrire(entrez le dernier quotient)
lire (q)
q-----q div s+ q mod s

Bonsoir hiba,

Tu n'as pas pris en compte les éléments de mon post précédent.
Diviseur 10, utilisation du reste et calcul du carré du reste.

@noemi pouvez vous me donner la réponse pour que je comprends ce que vous voulez dire

Bonjour hiba et bonjour Noemi,

Hiba, je te mets un exemple pour essayer de te faire comprendre le principe à utiliser (que Noemi t'a indiqué).
Tu ne pourras écrire l'algorithme que lorsque tu auras compris le principe.

Exemple : n=245

Soit S la somme des carrés des chiffres, qu'il faut calculer

Au départ, S=0

1ère étape : division euclidienne de n=245 par 10 (pose la division, si tu le souhaites)
n=245=(24 x 10) + 5
le reste est 5 qui est le chiffre des unités
S=5²=25

On répète le processus en prenant comme nouvelle valeur de n le quotient trouvé qui vaut 24

2ème étape :division euclidienne de n=24 par 10 (pose la division, si tu le souhaites)
n=24=(2x 10) + 5
le reste est 4 qui est le chiffre des dizaines
S=S+4²=25+4²=25+16=41

On répète le processus en prenant comme nouvelle valeur de n le quotient trouvé qui vaut 2

3ème étape : division euclidienne de n=2 par 10 (pose la division, si tu le souhaites)
n=2=(0x10)+2
le reste est 2 qui est le chiffre des centaines
S=S+2²= 41+2²=41+4=45

Le procédé doit s'arrêter car le quotient trouvé est 0

La 4ème étape (ainsi que les suivantes) serait la division euclidienne de n=0 par 10 (pose la division, si tu le souhaites)
n=0=(0x10)+0
le reste est 0 qui est le chiffre des milliers, des dizaines de milliers, ...
S=S+0²=45+0=45
etc , etc,...

La réponse finale cherchée est donc S=45

Essaie de comprendre cet exemple..
Pour être sûre de bien maîtriser le processus, tu peux faire d'autres exemples.
n=1762 => S=90
n=28461 => S=121

Ensuite, tu pourras passer à l'écriture du procédé (c'est à dire écrire l'algorithme)

Bon courage.

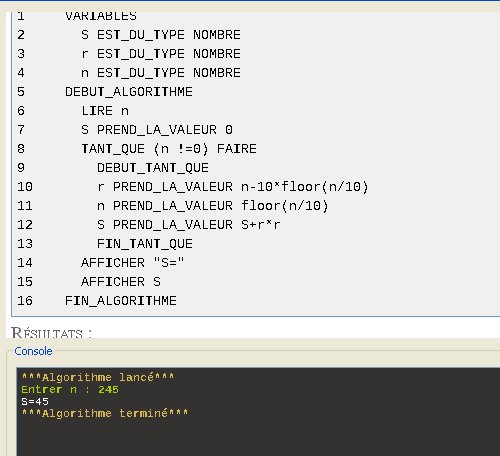
Pour donner une fin à ce topic, je mets un algorithme fait avec Algobox (logiciel gratuit qui permet d'écrire facilement des algorithmes et de les tester).

Certains codes ne sont pas du langage dit "naturel" mais sont spécifiques à Algobox :
n !=0 veut dire "n différent de 0"
floor(n/10) veut dire "quotient entier de n par 10"