Fonction affine par intervalle

[Markus]

Bonsoir !!!
#vp j'aimerais comprend comment Est-ce qu'on démontre qu'une fonction valeur absolu est affiche par intervalle.
Par exemple, pour f(x) =|3x-1|.
Je sais que :
-j'écris f(x) sans les valeurs absolu.
Soit... 2x-1=0
X=1/3
Ensuite...
Je suis bloqué !!!
Svp aidez moi

[Noemi]

Bonsoir Markus,

Tu résous 3x-1 > 0, soit pour x > 1/3
donc f(x) = 3x-1 si x > 1/3
et -3x+1 si x < 1/3
0 si x = 1/3

Tu peux inscrire ces résultats dans un tableau.

[karlnight]

@noemi a dit dans Fonction affine par intervalle :

Bonsoir Markus,

Tu résous 3x-1 > 0, soit pour x > 1/3
donc f(x) = 3x-1 si x > 1/3
et -3x+1 si x < 1/3
0 si x = 1/3

Tu peux inscrire ces résultats dans un tableau.

[mtschoon]

Bonjour,

Un petit plus, si besoin.
Markus , revois la définition de valeur absolue

Si $a\ge 0,|a|=a$
Si $a\le 0,|a|=-a$

Ici,il y a donc deux cas

1er cas : $3x-1\ge 0$ c'est à dire $x\ge \frac{1}{3}$
$\boxed{f\left(x\right)=3x-1}$

2ème cas : $3x-1\le 0$ c'est à dire $x\le \frac{1}{3}$
$\boxed{f\left(x\right)=-(3x-1)=-3x+1}$

Comme t'a dit Noemi, tu peux disposer ces réponses dans un tableau

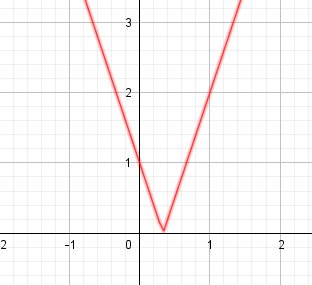
Tu peux aussi faire la représentation graphique de la fonction