Centre de gravité et vecteurs

[coca]

Bonjour,

J'ai résolu un exercice de maths avec les propriétés du collège mais je dois le faire avec les vecteurs
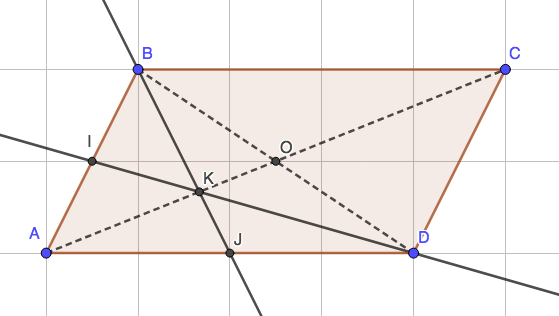
ABCD parallélogramme
I milieu de [AB] et J milieu de [AD]
K intersection de (JB) et (ID).
Montrer que A, K et D C sont alignés.
Merci de votre aide

[Noemi]

Bonsoir coca,

Ce sont les points A, K et C alignés ?
A quoi correspond le point K pour le triangle ABD ? quelle relation vectorielle peut-on écrire ?

[coca]

@noemi
Oui effectivement ce sont A K et C qui sont alignés (faute de frappe). K est le centre de gravité de ABD, mais ce n'est pas dit dans l'énoncé. C'est à nous de trouver les relations vectorielles.

[Noemi]

Bonjour coca
Tu places le point O intersection de (AC) et (DB). K est le point d'intersection des médianes donc vect AK = ....

[zipang]

[mtschoon]

Bonjour à tous,

Il est vrai que la méthode "collège" est vraiment la plus simple !

Pour la méthode vectorielle,coca, tu est tout de même obligé d'utiliser une propriété usuelle vu en collège...

(BJ) et (DI) sont deux médianes du triangle ABD.
Elles se coupent donc au point K centre de gravité de triangle ABD; K est situé sur [BJ] au 2/3 à partir du point B (et au 1/3 à partir du point J)
$\overrightarrow{BK}=\frac{2}{3}\overrightarrow{BJ}$

Avec la relation de Chasles,
$\overrightarrow{AK}=\overrightarrow{AB}+\overrightarrow{BK}$

donc
$\overrightarrow{AK}=\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BJ}$

Encore avec la relation de Chasles,
$\overrightarrow{AK}=\overrightarrow{AB}+\frac{2}{3}(\overrightarrow{BA}+\overrightarrow{AJ})$

En transformant
$\overrightarrow{AK}=\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AJ}$

En mettant 1/3 en facteur
$\overrightarrow{AK}=\frac{1}{3}(\overrightarrow{AB}+2\overrightarrow{AJ)}$

puis,
$\overrightarrow{AK}=\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AD})$

Je te laisse faire une dernière transformation qui te permettra de trouver
$\fbox{\overrightarrow {AK}=\frac{1}{3}\overrightarrow{AC}}$ et tirer la conclusion.