Récurrence ou pas et comment
-
Hhadeel_ dernière édition par mtschoon
pour n>=2 , montrer que 2n points et n²+1 segments forment au moins un triangle
-
Bonjour hadil-benyahia99,
Pour relier les points entre eux en formant un polygone, pour nnn points, on trace nnn segments, donc pour 2n2n2n points , 2n2n2n segments.
Si on souhaite au moins un triangle, il faut tracer un segment en plus soit 2n+12n+12n+1 segments.
Il reste à vérifier dans quelle condition n2+1≥2n+1n^2 + 1 \geq 2n+1n2+1≥2n+1Je te laisse résoudre cette inéquation.
-
Hhadeel_ dernière édition par
merci noemi pour votre attention
mais je n'arrive pas à comprendre pourquoi vérifier dans quelle condition n²+1>=2n+1
-
@hadil-benyahia99,
Pour être sur de tracer un triangle avec 2n points, il faut tracer 2n+1 segments,
comme l'énoncé indique n2n^2n2 + 1 segments il faut vérifier que le nombre de segments donnés est supérieur au nombre minimum nécessaire : soit que :
n2n^2n2 +1 ≥ 2nnn + 1
-
Hhadeel_ dernière édition par
alors merci beaucoup ... c'est génial de prouver des solutions de cette manière
-
Hhadeel_ dernière édition par
bonsoir @noemi
mon enseignant a dit qu'il y a une autre méthode pour montrer ça.. mais j n'arrive pas à la trouver ...
-
Bonjour @hadil-benyahia99
Tu peux faire une démonstration par récurrence.
-
mtschoon dernière édition par mtschoon

Bonjour Noemi et hadil.benyahia99,
Je regarde cet exercice et je trouve qu'il est plus subtile qu'il parait à première vue...
Si j'ai bien lu, l'énoncé donne, au départ, 2n points et n²+1 segments (le tout est déjà placé).
La question consiste à démontrer que, dans la configuration ainsi donnée, il y a au moins un triangle.Dans la solution ici proposée, avec les 2n+1 segments construits , on a bien au moins un triangle ( et le nombre 2n+1 est bien inférieur au nombre n²+1), mais (car il y a un "mais") , rien ne prouve que ces 2n+1 segments construits font partie des n²+1 segments placés au départ).
Je pense que c'est la raison pour laquelle le professeur demande une autre solution.
Effectivement, pourquoi pas une récurrence ?
-
Hhadeel_ dernière édition par
@mtschoon
Effectivement il a dit que c'est par récurence et que l'initialisation est un peu dure .... malheureusment il attend l'un des etudiants pour la prouver il ne va pas le corriger
-
mtschoon dernière édition par mtschoon

Bonsoir hadil.benyahia99,
C'est vrai que cette récurrence est assez délicate.
Ce soir, c'est trop tard.
Demain je prendrai le temps de te donner des pistes pour l'initialisation et la transmission, si tu en as besoin.
-
Hhadeel_ dernière édition par
@mtschoon
Merci ... j'en ai vraiment besoin
-
mtschoon dernière édition par mtschoon

Quelques idées possibles pour la récurrence,
Initialisation pour n=2
2n=4 et n²+1=5
Soit A,B,C,D les 4 points.
Avec 4 points, on peut former 6 segments .
Ce nombre 6 peut se trouver avec la formule des combinaisons , mais si les combinaisons ne font pas partie de ton programme, tu peux expliciter ces 6 segments [AB],[AC],[AD], BC],[BD],[CD]
Ici, il y a 5 segments donnés.
Tu peux déduire que 2 points ne sont pas liés entre eux.
Supposons que ces points non reliés soient A et B
Tu explicites les 5 segments existants et tu trouveras ainsi au moins un triangle.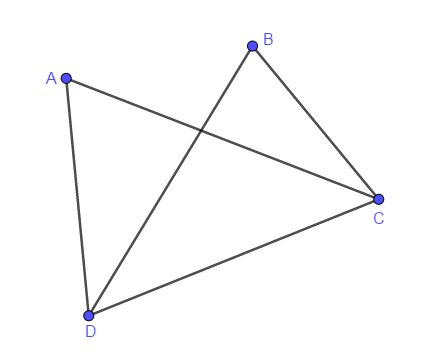
-
mtschoon dernière édition par mtschoon

Hérédité (ou Transmission, suivant ton vocabulaire)
Hypothèse à un ordre n (n≥2n \ge 2n≥2) : on suppose qu'il il a 2n points et n²+1 segments entre ces points et que les n²+1 points forment au moins un triangle
Pour 2(n+1) points et (n+1)²+1 segments entre ces points, il faut prouver qu'il y a au moins un triangle, en faisant intervenir l'hypothèse à l'ordre n.
Une idée (si tu n'en trouves pas d'autre) :
2(n+1)=2+2n
Soit A,B et 2n autres points.
Soit C un des 2n autres points.Il y a deux éventualités relatives à C (que l'on peut détailler) :
1ère éventualité : Pour au moins un point C, les segments [CA] et [CB] font partie des (n+1)²+1 segments donnés.
La conclusion est immédiate vu que l'on obtient le triangle ABC2ème éventualité : pour tout point C, il existe seulement 1 (ou 0) segment liant C avec A (ou B).
Parmi les (n+1)²+1 segments, (2n+1) est majorant du nombre de segments dont une (ou aucune) des extrémités est A (ou B)
Or [(n+1)²+1]-(2n+1)=n²+1
On peut déduire que l'on peut trouver n²+1 segments ayant leurs deux extrémités parmi les 2n points.
Avec l'hypothèse de la récurrence, on peut tirer la conclusion souhaitée (il y a au moins un triangle).Cette explication n'est pas simple...si tu en trouves une plus simple, ce sera encore mieux...
Bon courage !
-
Hhadeel_ dernière édition par
Merci @mtschoon mais franchement je veux comprendre si l'initialisation pour n=2 est lié á l'heredité ou bien c'est une autre idée.. merci pour votre attention
-
mtschoon dernière édition par zipang

Tu veux démontrer par récurrence une propriété vraie pour tout n≥2n \ge 2n≥2
Pour cela :
-
Tu dois prouver que cette propriété est vraie pour la valeur de n de départ, ici n=2
c'est l'initialisation (qui n'a rien à voir avec l'hérédité) -
Ensuite, tu dois prouver que si la propriété est vraie à un ordre n (n≥2n\ge 2n≥2) alors elle est vraie à l'ordre n+1
c'est l'hérédité (on dit aussi Transmission)
Lorsque 1 ) et 2) sont prouvés, tu peux conclure que la propriété est vraie pour tout n supérieur ou égal à 2
-
-
Hhadeel_ dernière édition par
@mtschoon j'espère que je vais lui expliquer ça clairement
-
mtschoon dernière édition par

@hadil-benyahia99 ,
Je te conseille de bien comprendre le principe de récurrence et de refaire seul l'exercice avant de l'expliquer à ton professeur.
Bon travail !
-
Hhadeel_ dernière édition par mtschoon
@mtschoon si je vais lui expliquer ce raisonnement, à tort, il ne vas pas accepter aucun autre raisonnement prochainement.. merci encore une fois
-
mtschoon dernière édition par

Tu pourras toujours lui expliquer plus tard, si aucune autre solution lui convient ...
Si tu maîtrises, c'est l'essentiel.Bonne continuation.
A+