Points sur une hyperbole-équation du second degré
-
LLua_air dernière édition par mtschoon
Bonjour,
C'est mon premier post sur ce forum
J'ai un devoir maison à rendre pour le 2 octobre, il y a deux exercices.
C'est surtout pour le deuxième exercice que je n'arrive pas à trouver : f(x)=1x−4+3f(x) =\frac{ 1}{x-4} +3f(x)=x−41+3
On considère l'hyperbole H représentation de la fonction f et le point A(3;4).Soit M le point de H d'abscisse x et N son symétrique par rapport à À.
On cherche à déterminer les positions possibles de M telles que N appartient à H.
-
Exprimer les coordonnées de N en fonction de x.
-
Démontrer que N appartient à H équivalent à dire que x2−6x+7=0x^2-6x+7 = 0x2−6x+7=0.
-
Conclure.
Voilà
(Je précise qu'on a vu que les équations de second degré cette année)
En espérant que vous pourrez m'aider
-
-
Bonjour Lua_air,
Question 1, Utilise le fait que le point A est le milieu du segment [MN]
soit xAx_AxA=xM+xN2\dfrac{x_M+x_N}{2}2xM+xN et
yAy_AyA=yM+yN2\dfrac{y_M+y_N}{2}2yM+yN
tu en déduis xNx_NxN et yNy_NyN en fonction de xxx.Question 2, si le point N appartient à H, alors f(xN)=yNf(x_N)=y_Nf(xN)=yN
Indique tes éléments de réponse si tu souhaites une vérification.
-
mtschoon dernière édition par

Bonjour Lua_air et Noemi,
Un petit plus si besoin,
Un schéma approximatif pour éclairer l'exercice,
(l'hyperbole est en rouge)
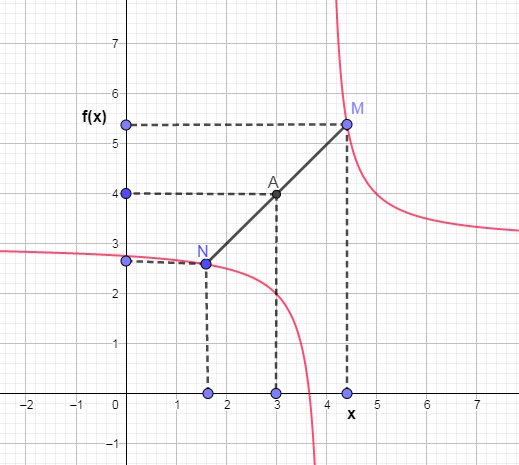
Notations :
xM=xx_M=xxM=x
yM=f(x)y_M=f(x)yM=f(x)
xA=3x_A=3xA=3
yA=4y_A=4yA=4
Ainsi, comme te l'a écrit Noemi :
x+xN2=3\frac{x+x_N}{2}=32x+xN=3 <=> xN+x=6x_N+x=6xN+x=6 <=> xN=....x_N=....xN=....
f(x)+yN2=4\frac{f(x)+y_N}{2}=42f(x)+yN=4 <=> yN+f(x)=8y_N+f(x)=8yN+f(x)=8 <=> yN=8−f(x)y_N=8-f(x)yN=8−f(x)<=> yN=....y_N=....yN=....Si tu as besoin, tiens nous au courant de l'avancé de ton exercice.
-
LLua_air dernière édition par mtschoon
Merci pour vos réponses
Je pense avoir compris ce que vous m'avez dit, mais à la question 2, je ne retrouve pas l'équation...Pour la question 1, j'ai trouvé :
xN=6−xx_N = 6-xxN=6−x
Mais mes résultats pour yNy_NyN ne cessent de changer (à chaque fois que je réessaye), donc je pense que le problème se situe là...
Pourriez-vous m'aider svp ?Merci d'avance
-
mtschoon dernière édition par mtschoon

Pour la question 1, tu dois trouver les expressions de xNx_NxN et yNy_NyN
Ce que tu donnes pour xNx_NxN est bon mais tu ne donnes pas yNy_NyN
yN=8−f(x)y_N=8-f(x)yN=8−f(x)
Il te reste à remplaces f(x) pas son expression:yN=8−(1x−4+3)y_N=8-(\frac{1}{x-4}+3)yN=8−(x−41+3)
Tu peux simplifier un peu en remplaçant 8-3 par 5, d'où$\fbox{y_N=5-\frac{1}{x-4}}$
Pour la question 2, Noemi t'a donné(e) la méthode :
$\fbox{f(x_N)=y_N}$Tu obtiendras ainsi une égalité qui, après transformations, te donnera :
x2−6x+7=0x^2-6x+7=0x2−6x+7=0
-
LLua_air dernière édition par mtschoon
Merci pour la réactivité
Alors pour la 2, j'ai trouvé :
9−5x2−x\dfrac{9-5x}{2-x}2−x9−5x
Est-ce que jusque là mon résultat est bon
-
mtschoon dernière édition par

Comme Noemi te l'a dit et que j'ai répété, tu dois écrire l'égalité f(xN)=yNf(x_N)=y_Nf(xN)=yN
Ce que tu donnes n'est pas une égalité.
f(xN)=1xN−4+3f(x_N)=\frac{1}{x_N-4}+3f(xN)=xN−41+3 et tu remplaces xNx_NxN par (6−x)(6-x)(6−x)
yN=5−1x−4y_N=5-\frac{1}{x-4}yN=5−x−41Ensuite, tu écris l'égalité.
-
LLua_air dernière édition par zipang
En marquant l'équation, je trouve :
f(6−x)=9−5x2−xf(6-x) = \dfrac{9-5x}{2-x}f(6−x)=2−x9−5x
-
mtschoon dernière édition par zipang

f(xN)=yNf(x_N)=y_Nf(xN)=yN équivaut à :
16−x−4+3=5−1x−4\dfrac{1}{6-x-4}+3=5-\dfrac{1}{x-4}6−x−41+3=5−x−41
Tu simplifies, tu transformes en des égalités équivalentes.
-
LLua_air dernière édition par mtschoon
Merci beaucoup pour votre aide, je suis finalement parvenue à l'équation demandée
(je n'avais en fait pas compris dans ce sens-là)Encore une fois merci, je ne sais pas ce que j'aurai fait sans vous
-
mtschoon dernière édition par mtschoon

De rien !
Nous sommes contentes de t'avoir aidé mais tu as aussi bien travaillé !
J'espère que tu as répondu à la question 3) qui consiste à résoudre l'équation trouvée à la question 2) (équation du second degré).
-
LLua_air dernière édition par mtschoon
Pas de soucis pour la 3, je l'avais résolu en avance et j'avais trouvé :
x1 = 3 - racine de 2
x2 = 3 + racine de 2(j'ai aucune idée de comment le taper donc je l'ai fait en l'écrivant)
Et du coup ce sont les deux positions possibles de M telles que N appartient à H
Encore une fois merci
-
mtschoon dernière édition par

C'est tout à fait ça.
( Le graphique que j'ai joint correspond approximativement à la valeur x2x_2x2 que tu indiques )Donc tout est bon.
-
LLua_air dernière édition par mtschoon
@mtschoon Alléluia
Merci
-
mtschoon dernière édition par mtschoon

Bonne continuation, Lua_air.
A+