Limite sans utiliser la règle l'Hôpital

Bonjour tous les membres de MATHFORU!
J'ai trouver une grande difficulté à résoudre cette question (de trouver la limite ) sans utiliser L'Hôpital
$lim⁡x→0x−tanxx−sinx\displaystyle \lim_{x\to 0} \frac{x-tanx}{x-sinx}$

Merci d'avance!

(formule re-écrite en Latex correct, pour plus de clareté)

Bonjour @mathématicienne !
Si ta fonction est bien $\dfrac{tan(x)}{x} - sin(x)$

En voici une courbe dans Geogebra (en vert)
Il y a aussi la courbe de ses composantes pour comprendre comment elles évoluent entre elles.
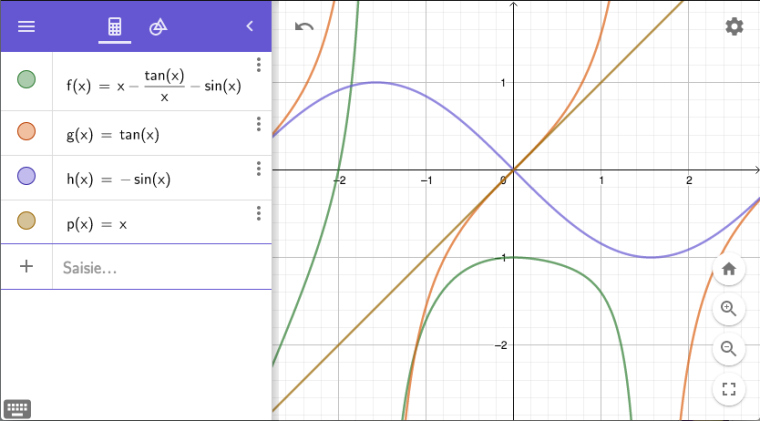
Etude limite f(x)

Cela doit donc te donner plus qu'un élément de réponse...!

Ce qu'il est intéressant d'observer c'est que l'étude de ta fonction revient à l'étude de $limx→0:tan(x)xlim_{x\to0} : \dfrac{tan(x)}{x}$

@zipang excuse-moi mais c'est pas ma fonction
Voilà ce que je cherche :
f(x) = (x-tanx)/(x-sinx)
Je pense que comme ça est mieux !

(J'ai déjà inséré les parenthèses mais ils n'apparaissent pas !)

Bonjour @mathématicienne,

Connais tu les développements limités ou une approximation de sin x et tan x en fonction de x au voisinage de 0 ?

@noemi non !
Pouvez-vous m'expliquer ?

@mathématicienne

Au voisinage de 0 ;
$sinx≈x−x36sinx\approx x-\dfrac{x^3}{6}$ et
$tanx≈x+x33tanx\approx x+\dfrac{x^3}{3}$

tu appliques à f(x) et tu peux en déduire une limite égale à -2.

@noemi mais je ne peux pas utiliser cette méthode ! (je pense que c'est après le bac )

Bonjour à tous,

Mathématicienne, pour les parenthèses qui n'ont pas été affichées dans ton premier message, je pense avoir une explication.

Tu as voulu écrire la formule en Latex (ce qui est très bien).

Pour que les parenthèses apparaissent, tu dois mettre un anti-slash avant chaque parenthèse, (la formule étant entre $ et $ bien sûr)

Evidemment, avec la fonction que tu as écrite sans les parenthèses, et dont zipang a fait un beau schéma, la limite était simple :
$lim⁡x→0[x−sinx]=0\displaystyle \lim_{x\to 0}[x -sinx]=0$
$lim⁡x→0tanxx=1\displaystyle \lim_{x\to 0}\frac{tanx}{x}=1$
donc
$lim⁡x→0[x−tan(x)x−sinx]=−1\displaystyle \lim_{x\to 0}[x-\frac{tan(x)}{x}-sinx]=-1$

La réponse se voit sur la courbe.

Pour ce qui est de la fonction que tu proposes, j'essayerai de trouver une solution sans DL et sans règle de l'Hôpital (méthodes effectivement post-Bac) lorsque j'aurais un peu de temps, mais elle ne sera pas simple...!

Je me pose des questions sur ce sujet
Est-ce un DM dans lequel il y a des questions préliminaires servant d'outils à la recherche de cette limite ?
Dans ce cas, il faudrait donner tout l'énoncé,
Sinon, est-ce une question BONUS pour les "forts en maths" ou bien une question de concours ou bien ... ?

Cela me parait bien difficile pour un exercice ordinaire sans questions préalables....

Je t'indique une voie possible(certainement parmi d'autres) si tu n'as aucune indication,

Pré-requis : limites usuelles et formules d'addition
il faut calculer sin(3a) et tan(3a) :
pour cela, partir de sin(a+b) déduire sin(2a) puis sin (2a+a)=sin(3a)
Idem pour tan(3a)
on doit trouver :
$\fbox{sin(3a)=3sina-4sin^3a}$
$\fbox{tan(3a)=\frac{3tana-tan^3a}{1-3tan^2a}}$

Idée : Diviser numérateur et numérateur de la fonction par $x^3$
(j'ai tenté de diviser par x , par x², mais ça ne donne rien de bon)

$\fbox{\frac{x-tanx}{x-sinx}=\frac{\frac{x-tanx}{x^3}}{\frac{x-sinx}{x^3}}}$

Soit $\frac{x-tanx}{x^3}$

Soit $l_1$ la limite de f lorsque x tend vers 0
en théorie, il faudrait justifier (par étude de fonction, encadrements..) que $l_1$ est un réel (non + $∞\infty$ ou - $∞\infty$ )

Changement d'inconnue $X=x3X=\frac{x}{3}$ c'est à dire $x = 3 X$
"x tend vers 0" équivaut à "X tend vers 0"

donc $l1=lim⁡X→03X−tan(3X)27X3\displaystyle l_1=\lim_{X\to 0}\frac{3X-tan(3X)}{27X^3}$

Soit $F(X)=3X−tan(3X)27X3F(X)=\frac{3X-tan(3X)}{27X^3}$

En transformant , on trouve
$F(X)=11−3tan2X[3(X−tanX)27X3−9Xtan2X27X3+tan3X27X3]F(X)=\frac{1}{1-3tan^2X}[\frac{3(X-tanX)}{27X^3}-\frac{9Xtan^2X}{27X^3}+\frac{tan^3X}{27X^3}]$

En améliorant :
$F(X)=11−3tan2X[327(F(X)−927(tanxX)2+127(tanXX)3]F(X)=\frac{1}{1-3tan^2X}\biggl[\frac{3}{27}\biggl(F(X)-\frac{9}{27}\biggl(\frac{tanx}{X}\biggl)^2+\frac{1}{27}\biggl(\frac{tanX}{X}\biggl)^3\biggl]$

Par passage à la limite , lorsque X tend vers 0, on obtient, après quelques simplifications l'égalité
$l1=19l1−13+127l_1=\frac{1}{9}l_1-\frac{1}{3}+\frac{1}{27}$
Après résolution de cette équation : $\fbox{l_1=-\frac{1}{3}}$

Soit $g(x)=x−sinxx3g(x)=\frac{x-sinx}{x^3}$

Même principe que pour f

Soit $l_2$ la limite de g lorsque x tend vers 0

On arrive à l'équation; $l2=19l2+427l_2=\frac{1}{9}l_2+\frac{4}{27}$

Après résolution : $\fbox{l_2=\frac{1}{6}}$

Conclusion :

la limite cherchée est : $\fbox{\frac{l_1}{l_2}=\frac{\frac{-1}{3}}{\frac{1}{6}}=-2}$

Bon courage ( il en faut ! ! !)

@mtschoon je ne sais pas comment vous remercier pour votre aide, vous m'aidez toujours à résoudre les difficiles questions (et pour répondre à votre question; non, il n'y a pas des questions préliminaires servant d'outils à la recherche de cette limite ) je pense que c'est bon pour nous, comme des élèves du sciences maths, de essayer de résoudre quelques " Questions de Défi" comme ça, et connaître leur astuce, j'aime beaucoup ça!
Merciiii encore !!!

De rien mathématicienne !
C'est avec plaisir que nous venons apporter de l'aide.
Je t'ai indiqué des grandes lignes mais il te reste beaucoup de travail pour mener tout cela à bien...c'est effectivement un petit défi pour traiter cet exercice en TS !
C'est un bel entraînement.
(Avec les formules de Bac+1, c'est beaucoup plus facile...)

@mtschoon (j'ai une question hors-sujet ) Pouvez-vous m'indiquer une bonne série d'exercices de T.V.I. (j'ai en trouvé beaucoup mais je veux quelque chose de haut niveau, c'est la seule chose qui me reste pour bien comprendre cette leçon (limites et continuité ) )

@Mathématicienne
Je te mets un lien où il y a un peu de tout, mais le TVI n'est pas très exigeant en niveau...

https://www.sos-devoirs-corriges.com/images/exercices-corriges-maths/lycee-terminaleS/theoreme-des-valeurs-intermediaires-continuite-exercices-corriges.pdf

Tu peux consulter pour voir si tu maîtrises bien.

Bonne lecture !

Merci beaucoup @mtschoon !
Je vais maintenant commencer le travail

Très bon travail, Mathématicienne !