excercice maths sur le repère orthonormé

bonjour,
je suis une maman qui doit expliquer à son fils un devoir mais j'avoue que j'ai du mal à lui répondre.
pouvez vous m'expliquer l’exercice
(0;i,j) est un repère orthonormé du plan. on considère le A=(-1;0) et B=(b;0) ou b est un nombre réel est positif. le demi-cercle [AB] situé au dessus de(0i) coupe la droite (oj) en T. objectif calculer (0T)
a)choisir b ok on a choisi 3
b)calculer les coordonnées du centre de ce demi-cercle
c)calculer la longueur du rayon de ce demi-cercle
d)en vous plaçant dans le triangle bien choisi, déterminer la longueur 0T
POUVEZ VOUS m'expliquer SVP

Bonjour kikounette,

Faire une figure, cela permet de vérifier les résultats.

b) Le centre, que je nomme C, du demi cercle se situe au milieu du diamètre donc le milieu du segment [AB]
Pour calculer les coordonnées du milieu d'un segment [AB], on applique
pour l'abscisse : $xC=xA+xB2x_C= \dfrac{x_A+x_B}{2}$ soit $xC=−1+32x_C= \dfrac{-1+3}{2}$ = ...
pour l'ordonnée : $yC=yA+yB2y_C= \dfrac{y_A+y_B}{2}$ soit $y_C = ......$

c) La longueur du rayon correspond à la longueur du segment CB
On calcule les coordonnées du vecteurs CB puis sa norme.

d) Pour le calcul de la longueur OT, On utilise le triangle TOC rectangle en O et on applique le théorème de Pythagore.

Voici quelques indications, vous pouvez proposer vos réponses ou calculs pour correction.

@noemi merci Noémi

Demain, j'essaye d'expliquer à mon fils
Je vous tiens au courant ️

Bonjour kikounette et Noemi,

Je m'interroge sur cet énoncé...

Pour faire le dessin, il faut bien sûr fixer une valeur de b (nombre réel positif).

Mais les calculs doivent-ils être faits avec la valeur numérique donnée à b ou doivent -ils être faits de façon générale en fonction de b ?

J'opterais pour le calcul général (calculs avec b)
Si c'est un DM à rendre et si le professeur doit vérifier les calculs des élèves , chacun ayant choisi une valeur à sa guise, le professeur aura du travail ! ! !
Et même si c'est pour faire une correction au tableau, ça lui posera problème !

kikounette, il me semble qu'il serait bon de regarder précisément la formulation de l'énoncé ou obtenir l'information auprès du professeur.

Bonjour mtschoom,

L'énoncé dit :choisir une valeur pour b puis faire une figure

Mes années d'études sont loin ️, je ne comprends rien..mais je vais essayer d'expliquer le mieux possible afin que mon fils s'améliore en maths..c'est un devoir facultatif mais je veux qu'il le fasse.

Bonjour kikounette,

Vous pouvez réaliser l'exercice en deux étapes.
D'abord étude du cas particulier avec b = 3.
puis étude du cas général.

Bonjour kikounette,

Comme je l'ai indiqué, je suis pratiquement sûre que "choisir une valeur pour b" s'applique à la figure, mais que les calculs demandés ensuite sont à faire avec un b quelconque.
Sinon, l'énoncé donnerait directement, comme pour A, des valeurs numériques pour les coordonnées de B.

Mais, comme l'indique Noemi, faire d'abord le cas particulier b=3 puis ensuite le cas général , sera très bien.
Ce sera un excellent entraînement.

Comme j'ai un peu de temps, voici quelques détails pour l'exemple $b=3\fbox{b=3}$
(voir d'abord les pistes de Noemi)
a)

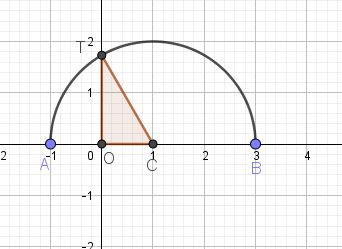
b)
$xC=−1+32=22=1x_C=\frac{-1+3}{2}=\frac{2}{2}=1$
$yC=0+02=02=0y_C=\frac{0+0}{2}=\frac{0}{2}=0$
Donc C a pour coordonnées (1,0)
c)
rayon=CB= $x_B-x_C|=|3-1|=2$
d)
Théorème de Pythagore dans le triangle OCT rectangle en O
$\fbox{OT^2+OC^2=CT^2}$
Or
$O C = 1$
$C T = r a y o n = 2$
Donc
$OT^2+1^2=2^2$
$OT^2+1=4$
$OT^2=4-1=3$
Conclusion
$\fbox{OT=\sqrt 3}$
(Une valeur approchée de $3\sqrt 3$ est 1.732.
On peut vérifier approximativement cette valeur sur le schéma)

Ceci correspondant seulement à l'exemple b=3, calculs sans doute non demandés par l'énoncé.
Mais, commencer par un exemple permet de mieux comprendre.

Lorsque cela est compris, il faut répondre aux questions en faisant les mêmes calculs avec b (sans donner de valeur précise à b, sachant seulement que b est un réel positif)

Bon travail.

@mtschoon

Merci

Mon fils a dû se tromper car il a trouvé :

Ot=1,5

Du coup le résultat est √,3,25️

Ce qui est écrit est inexact et incohérent.
$3.25≈1.8\sqrt{3.25} \approx 1.8$ donc $3.25≠1.5\sqrt{3.25} \ne 1.5$

Une seule chose à faire : dire à votre fils de consulter ce topic vu que le calcul de OT, égal à $3\sqrt 3$ , y est détaillé.

Il peut, bien sûr, taper ses calculs ici, et nous vérifierons.

Bon travail à lui.

@mtschoon

Merci mtschoon,
Je ne vais pas lui donner les réponses, il va refaire son exercice et je vais essayer de lui expliquer au fur et à mesure grâce à vos résultats et aux explications de Noémi..
Comme ça, il fera son deuxième exercice peut être plus facilement.

En tout cas un grand Merci à vous tous pour le temps que vous nous consacrez.

@kikounette,

Bonne décision de donner une explication pas à pas. Vous pouvez aussi lui demander de refaire les calculs avec une autre valeur de b.
Vous pouvez aussi indiquer sur ce topic ses calculs afin que l'on voit ses erreurs et que l'on puisses éventuellement lui fournir des éléments de remédiation.

@kikounette

Bon courage !