Aide devoir maison vecteurs

[Rin]

Bonjour ! Voilà j'ai un DM à rendre lundi, je bloque sur le dernier exercice. Le voici !

Scan supprimé

Pour ce qui est de la première question, j'ai trouvé que le vecteur AN : 2/3 du vecteur AC. Mais je n'ai aucune idée de comment le démontrer avec la relation de Chasles... je l'ai trouvé au hasard... Et je n'ai pas réussi les questions suivantes

[Noemi]

Bonjour Rin,

Le scan de l'énoncé est interdit sur ce forum, seul les schémas ou graphiques sont autorisés.
Le scan va être supprimé.
Recopie l'énoncé pour obtenir une aide.

Utilise la deuxième relation pour répondre à la première question.

[Rin]

@noemi oh je ne savais pas, je ne comprends pas pourquoi mais d'accord.

[Noemi]

@rin,

Tu peux écrire l'énoncé question par question.
La relation de Charles c'est par exemple :
$\overrightarrow{CN}$ = $\overrightarrow{CA}$ + $\overrightarrow{AN}$

[Rin]

"Soit ABC un triangle, on définit M, N et P par :
$\overrightarrow{AM}$ = 2/5$\overrightarrow{AB}$ ; $\overrightarrow{NA}$ - 2$\overrightarrow{CN}$ = $\overrightarrow{0}$ et $\overrightarrow{PC}$ = -1/2$\overrightarrow{BC}$"

"A l'aide de la relation de Chasles, exprimer le vecteur AN en fonction de AC. Faire une figure."

J'ai trouvé par pur hasard que NA = 2/3AC mais je ne sais pas du tout comment le démontrer avec la relation de Chasles...

[Noemi]

Bonjour rin,

A partir de la relation : $\overrightarrow{NA}$ - $2\overrightarrow{CN}$ = $\overrightarrow{0}$
$\overrightarrow{NA}$ - $2\overrightarrow{CA}$ - $2\overrightarrow{AN}$= $\overrightarrow{0}$
puis :
$3\overrightarrow{AN}$ = $2\overrightarrow{AC}$
d'où : $\overrightarrow{AN}$ = ....

[Rin]

@noemi comment tu es passé de NA -2CN -2AN à 3AN ?...

[Noemi]

@rin,

$\overrightarrow{NA}$ - $2\overrightarrow{CA}$ - $2\overrightarrow{AN}$= $\overrightarrow{0}$
Or $\overrightarrow{NA}$= - $\overrightarrow{AN}$
donc -$\overrightarrow{AN}$ - $2\overrightarrow{CA}$ - $2\overrightarrow{AN}$= $\overrightarrow{0}$
alors - $2\overrightarrow{CA}$ - $3\overrightarrow{AN}$= $\overrightarrow{0}$
Donc $2\overrightarrow{CA}$ + $3\overrightarrow{AN}$= $\overrightarrow{0}$
alors $3\overrightarrow{AN}$= - $2\overrightarrow{CA}$
$3\overrightarrow{AN}$= $2\overrightarrow{AC}$
car : $\overrightarrow{CA}$= - $\overrightarrow{AC}$

[Rin]

@noemi oh je vois merci beaucoup!

[Rin]

Pour la figure j'ai fait ceci

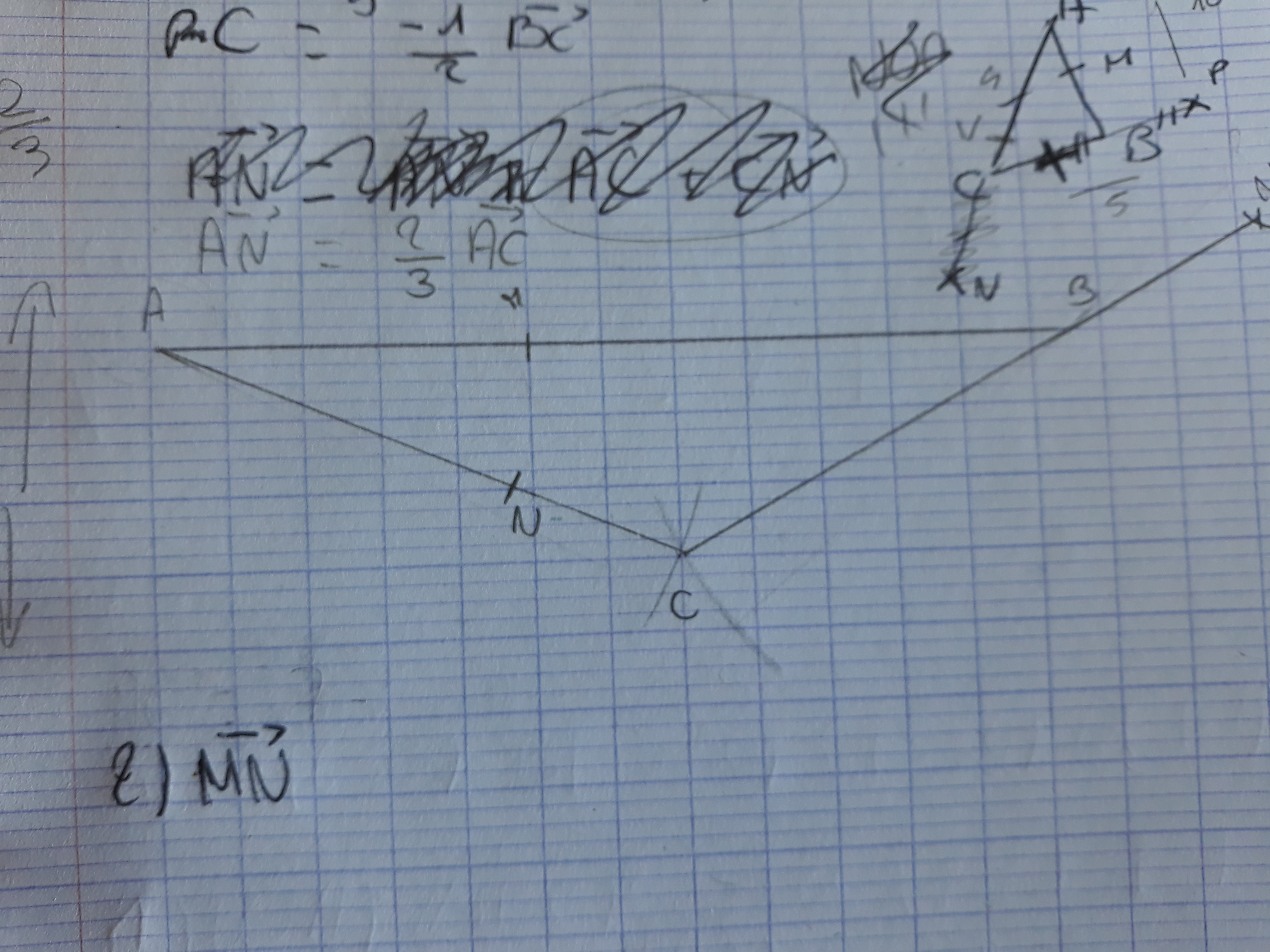
Avec AB = 10cm ; BC = 5cm ; AC = 6cm ; AM = 4cm ; AN = 4cm et BC = 2,5cm

[Noemi]

@rin,

Le point P est mal placé.
c'est $\overrightarrow{PC}$= $-\frac{1}{2}$ $\overrightarrow{BC}$
Ou
$\overrightarrow{PC}$= $\frac{1}{2}$ $\overrightarrow{CB}$
Donc le point P est avant le point C sur la droite (CB).

[Rin]

@noemi d'accord merci !!

Pour la question deux (vraiment désolé je ne comprends vraiment rien) je dois exprimer MN et MP en fonction de AB et AC...

[Noemi]

@rin

Utilises la relation :
$\overrightarrow{AM}$= $\frac{2}{5}$ $\overrightarrow{AB}$
Soit $\overrightarrow{AN}$ + $\overrightarrow{NM}$= $\frac{2}{5}$ $\overrightarrow{AB}$
Tu utilises ensuite la valeur trouver pour le vecteur $\overrightarrow{AN}$ et tu en déduis le vecteur $\overrightarrow{MN}$

Pour le vecteur $\overrightarrow{MP}$, utilise la dernière relation.

A partir des relations des deux vecteurs, tu réponds à la dernière question.

[Rin]

@noemi d'accord merci beaucoup!!