Recherche de fonctions inverses.
-
?Un Ancien Utilisateur dernière édition par mtschoon
Bonsoir tout le monde!
J'ai une question concernant la fonction inverse donc, j'ai répondu au premières questions :
~ La fonction est f(x)=arctan((x2−1)/(2x))f{(x)}=arctan{({(x^2-1)}/{(2x)})}f(x)=arctan((x2−1)/(2x))- montrer que f est paire ( c'est fait )
*Calculer la limite de f(x) à 0+ et +infini (jai trouvé -pi/2 pour la 1ère et pi/2 pour la 2ème) - prouvé que f est bijection de ]0,+oo[ à J (c'est aussi fait; j'ai trouvé que J=]-pi/2,pi/2[ )
Et donc voilà ce que je cherche : *trouver la fonction inverse f−1f^-1f−1 pour tout x appartient à J .
Merci d'avance!
- montrer que f est paire ( c'est fait )
-
mtschoon dernière édition par mtschoon

Mathématicienne , bonjour,
Oui pour tes réponses.
Avec les intervalles adaptés, la fonction arctan est la réciproque de la fonction tan
la fonction tan est la réciproque de la fonction arctan.Piste de calcul pour x=f−1(y)x=f^{-1}(y)x=f−1(y)
y∈]−π2,π2[y \in ]-\frac{\pi}{2},\frac{\pi}{2}[y∈]−2π,2π[ et x∈]0,+∞[x\in ]0,+\infty[x∈]0,+∞[
y=arctan(x2−12x)y=arctan(\frac{x^2-1}{2x})y=arctan(2xx2−1)
x2−12x=tany\frac{x^2-1}{2x}=tany2xx2−1=tany
x2−1=2xtanyx^2-1=2xtanyx2−1=2xtany
x2−2xtany−1=0x^2-2xtany-1=0x2−2xtany−1=0
Tu as une équation du second degré d'inconnue x à résoudre (et vu l'intervalle , tu conserveras la solution positive)
Lorsque tu auras terminé le calcul, pour la conclusion, tu pourras échanger le notations x et y pour redonner à x son rôle de variable indépendante.
Si tu préfères, tu peux changer les notations dès le début du calcul.
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
@mtschoon solution trouvée, merci beaucoup!
Une autre question s'il vous plaît!
La fonction inverse de f(x)=x(2−x)f{(x)}=\dfrac{x}{(2-\sqrt{x})}f(x)=(2−x)x
Tel que f (x)------> f (x)^-1
[0,4 [ -------> [0,+oo[
-
Bonsoir @mathématicienne,
Comme xxx ≥ 0
Fait un changement de variable uuu = x\sqrt xx puis tu résous l'équation du second degré.
-
?Un Ancien Utilisateur dernière édition par
@noemi oh d'accord c'est clair, est-ce-que toujours on doit rendre l'équation sous forme d'équation du deuxième degré pour trouver la fonction inverse?
-
@mathématicienne,
Non, tu transformes pour trouver xxx en fonction yyy et tu analyses l'équation.
-
?Un Ancien Utilisateur dernière édition par
@noemi d'accord c'est compris! Merci beaucoup!
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
@noemi a dit dans La fonction inverse de arctan((x^2-1)/(2x)) :
@mathématicienne,
Non, tu transformes pour trouver xxx en fonction yyy et tu analyses l'équation.
J'ai trouvé deux solutions
U1=(-x-sqrt(x^2+4))/2 < 0 (n'est pas une solution )
U2=(-x+sqrt(x^2+4))/2
Mais je ne sais pas comment montrer que U2 appartient à [0,2[
-
@mathématicienne
Vérifie les calculs.
si tu poses u=xu = \sqrt xu=x ensuite il faut élever au carré pour écrire xxx en fonction de yyy.
-
mtschoon dernière édition par

@Mathématicienne Bonsoir (et Bonsoir Noemi)
Je regarde l'énoncé de ta seconde question et ne déchiffre pas clairement.
Que veux-tu dire par : [0,4 [ -------> [0,+oo[ ?
Merci pour l'indication.
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
Bonsoir @mtschoon !
je veux dire que
f(x)f(x)f(x) est définie sur [0,4 [
Et f−1(x)f^{-1}(x)f−1(x) est définie sur [0,+oo [
-
mtschoon dernière édition par mtschoon

@Mathématicienne
Merci pour ton indication
Une remarque : n'écris pas f(x)−1f(x)^{-1}f(x)−1 mais f−1(x)f^{-1}(x)f−1(x)
Si tu es sûre des deux intervalles que tu indiques, l'expression que tu donnes pour f(x) est fausse.
Tu donnes f(x)=x1−xf(x)=\frac{x}{1-\sqrt x}f(x)=1−xx
Cette fonction est définie sur R-{1}
Etudie la de près.
Elle ne définie absolument pas une bijective de [0,4[ vers [0,+∞[[0,+\infty[[0,+∞[
En 1 ( valeur interdite) il y a deux limites (à droite et à gauche )valant +∞+\infty+∞ et −∞-\infty−∞ et pour x >1 elle prend des valeurs négatives.
Cela explique que tu n'aies pas pu aboutir (avec u compris entre 0 et 2, dans tes calculs précédents)Avec cette fonction, pour trouver une bijection et définir sa bijection réciproque , il aurait fallu prendre [0,1[ au lieu de [0,4[
-
mtschoon dernière édition par mtschoon

Comme indiqué ci-dessus, si tu es sûre de [0,4[ vers [0,+∞+\infty+∞[,il faut changer de fonction f
En prenant, par exemple, $\fbox{ f(x)=\frac{x}{2-\sqrt x}}$, on peut définir une bijection de [0,4[ vers [0,+∞\infty∞[
Ainsi, tu peux vraiment trouver f−1f^{-1} f−1bijection réciproque de f, de [0,+∞\infty∞[ vers [0,4[Alors, regarde ton énoncé de près et refais les calculs car il faut que tu changes, ou bien un intervalle, ou bien la fonction
Tiens nous au courant si besoin.
-
mtschoon dernière édition par mtschoon

Pour le cas (?) où il s'agirait de ma seconde proposition (ce que j'ignore),
$\fbox{f(x)=\frac{x}{2-\sqrt x}}$ de [0,4[ vers [0,+∞\infty∞[, je te donne la réponse pour f−1f^{-1}f−1 pour pouvoir vérifier les calculsEn résolvant y=x2−xy=\frac{x}{2-\sqrt x}y=2−xx d'inconnue x après produit en croix, changement d'inconnue, choix entre les deux solutions et élévation au cas, tu dois trouver
x=(y−y2+8y)24x=\frac{(y-\sqrt{y^2+8y})^2}{4}x=4(y−y2+8y)2Pour la conclusion, en redonnant à x sa fonction de variable indépendante, tu dois obtenir
f−1f^{-1}f−1 bijection de [0,+∞\infty∞[ vers [0,4[ défine par :
$\displaystyle \fbox{f^{-1}(x)=\frac{(x-\sqrt{x^2+8x})^2}{4}}$Si tu représentes ces deux bijections f et f−1f^{-1}f−1(sur leurs intervalles respectifs) dans un repère orthonormé, tu constateras, ce qui est une propriété usuelle, que les deux représentations graphiques sont symétriques par rapport à la droite d'équation y=x
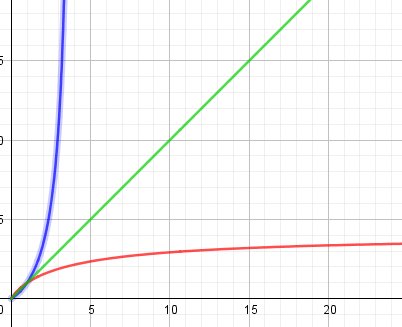
(f est en bleu, f−1f^{-1}f−1 est en rouge, y=x est en vert)
-
?Un Ancien Utilisateur dernière édition par Un Ancien Utilisateur
@mtschoon oui, c'est une grande faute!!! Excusez-moi
 j'ai corrigé ça. (c'est ce qui se passe lorsque vous étudiez à 23 h)
j'ai corrigé ça. (c'est ce qui se passe lorsque vous étudiez à 23 h)
Excusez-moi encore .
Et ouii vous avez raison
La fonction correcte est f(x)=x(2−x)f{(x)}=\dfrac{x}{(2-\sqrt{x})}f(x)=(2−x)x
Après les calculs j'ai trouvé le même résultat de f−1(x)f^{-1}{(x)}f−1(x)
-
mtschoon dernière édition par

Pas grave, Mathématicienne
 ,
,
Je n'ai pas travaillé pour rien vu que j'ai pris la "bonne" fonction.
Tu as très bien travaillé toi aussi vu que tu as trouvé f−1(x)f^{-1}(x)f−1(x)