lecture graphique(limite d'une fonction)

salut!
j'arrive pas à comprendre comment peut on trouver la
lim f(x)/x en l'infinie graphiquement aidez moi svp

Bonsoir saraSBH,

Tu disposes de quel graphique ? celui de f(x) ou celui de f(x)/x ?

Bonsoir Noemi,
celui de f(x) et il me demande de trouver f(x) en + l'infinie puis f(x)/x
en + l'infine et moi je trouve une FI puisque la lim f(x) en + l'infinie est égale à - l'infinie et lim f(x)/x en + l'infinie ça devient l'infinie sur l'infinie

Tu as l'expression de f(x) ?
Peux-tu transmettre la représentation graphique de la fonction ?

@noemi j'ai pas l'expression seulement une courbe

(graphique modifié pour supprimer le texte)

Bonsoir saraSBH iet noemi,

@saraSBH

Piste,

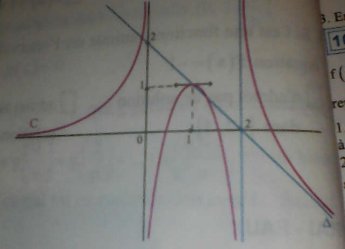
Dans ton graphique, tu n'as pas que la courbe, tu as aussi les asymptotes
En $+∞+\infty$ , tu as une asymptote oblique dont tu peux trouver le coefficient directeur par lecture graphique

Je te laisse trouver le lien entre $lim⁡x→+∞f(x)x\displaystyle \lim_{x\to +\infty} \frac{f(x)}{x}$ et le coefficient directeur de l'asymptote oblique.

Remarque : j'ai découpé ton graphique car ici, on doit donner les graphiques sans texte.

@mtschoon @Noemi merci infiniment

@mtschoon
quand on a pas d'asymptote oblique comment peut l'a déduire graphiquement
si c'est une branche parabolique?

J'espère que tu as trouvé -1 pour la limite en $+∞+\infty$ de $f(x)x\frac{f(x)}{x}$

S'il n'y a pas d'asymptote oblique, déduire, seulement graphiquement, qu'il y a branche parabolique, n'est vraiment pas commode !
.
On peut 'observer le mieux possible la courbe et tenter de deviner la "direction" de la branche infinie, mais cela n'est pas rigoureux.

L'énoncé ne t'aurait pas poser la question dans ce cas.

j'ai calculer la pente de l'asymptote oblique et je l'ai bien trouvé -1
toute est plus claire maintenant . grand merci !

C'est bien ça pour la pente a de l'asymptote oblique : $a=-1\fbox{a=-1}$

Pour justifier que $\fbox{\displaystyle \lim_{x\to +\infty} \frac{f(x)}{x}=-1}$, tout dépend de ton cours.

Si ton cours indique que l'équation de l'asymptote oblique est $y = a x + b$ avec $a=lim⁡x→+∞f(x)xa=\displaystyle \lim_{x\to +\infty} \frac{f(x)}{x}$ et $b=lim⁡x→+∞[f(x)−ax]\displaystyle b=\lim_{x\to +\infty}[ f(x)-ax]$ , tu n'a rien à faire de plus.

Si ton cours t'indique seulement la définition de l'asymptote oblique $[f(x)−(ax+b)]=0\displaystyle\lim_{x\to +\infty} \ [f(x)-(ax+b)]=0$ , il faut alors que tu démontres, en partant de cette définition, que $lim⁡x→+∞f(x)x=a\displaystyle \lim_{x\to +\infty} \frac{f(x)}{x}=a$

A toi de voir en fonction de ton cours.