Suite non convergence U(n)=sin(n)

[viennux]

bonjour,
je suis bloquée sur le dernier exercice de ma fiche et j'aurais besoin d'aide svp :

On considère la suite (Un) définie pour tout entier n par Un= sin(n) et l un réel
En raisonnant par l'absurde et en utilisant l'intervalle ouvert l- 1/4; l+1/4. : démontrer que la suite (Un) ne converge pas vers l

J'ai réfléchit et je pensais montrer que cette propriété (que l'on nommerait avant) est vraie (soit elle ne converge pas) puis que le contraire est aussi vrai (soit elle converge) et donc montrer la contradiction.
Cependant, je ne sais pas comment m'y prendre algébriquement.
comment doit on utiliser sin(n), sachant qu'elle est périodique de période 2PI
merci d'avance

[Noemi]

Bonjour viennux,

Utilise les formules de trigonométrie,
calcule sin(n+1/4) - sin(n-1/4) =

[viennux]

on peut pas plutôt utiliser sin(a)sin(b) + cos(a)cos(b)
je ne comprends pas comment s'y prendre avec le calcul (par l'absurde) pourriez vous m'expliquer ?

[viennux]

et dans la formule sin(n+1/4) - sin(n-1/4)
pourquoi on soustrait ?

[Noemi]

Bonjour viennux,
Si tu utilises sin(n+1) - sin(n-1) = 2 sin 1 cos n
Comme on a supposé que lim sin n = l, cela conduit à lim cos n = 0.

sin(n+1) = cos1 sin n + cos n sin 1,
la limite de sin (n+1) = l cos 1
A partir de l'unicité de la limite tu déduis l = l cos 1, soit l(1 - cos1) = 0, soit l = 0

Ensuite il faut trouver une contradiction :
or $si{n}^{2}n+co{s}^{2}n=1$
lim $si{n}^{2}n+co{s}^{2}n=1$ et lim $si{n}^{2}n+co{s}^{2}n=0$
donc .....

[mtschoon]

Bonjour,

Je regarde un peu l'énoncé proposé et la discussion qui me laisse perplexe.

Il est demandé un raisonnement par l'absurde, en utilisant l'intervalle ouvert ]L- 1/4; L+1/4[

Voici une proposition alternative, en tenant compte de l'énoncé.

Piste à expliciter soigneusement (ce n'est qu'une piste)

Supposons que la suite (sin(n)) converge vers L
Par définition , cela veut dire que :
Pour tout $ϵ\ge 0$, il existe N naturel tel que pour tout $n>N,|sin(n)-L|<ϵ$
En particulier , pour $ϵ=\frac{1}{4}$
Il existe N naturel tel que pour tout $\fbox{n\gt N}$, $|sin(n)-L|<\frac{1}{4}$, c'est à dire $\fbox{L-\frac{1}{4} \lt sin(n) \lt L+\frac{1}{4}}$

Prouvons que c'est impossible
L'intervalle ]L-1/4, L+1/4[ a une amplitude de 1/4-(-1/4)=1/2
L'intervalle relatif à ((sin(n)) a une amplitude de 1-(-1)=2
C'est là qu'on doit trouver une contradiction avec l'hypothèse de convergence vers L

Schéma :

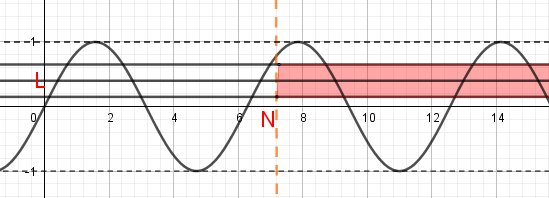
La zone en rouge, pour n>N, est la bande comprise entre y=L-1/4 et y= L+1/4
Dans le schéma joint, pour n > N, tous les termes sin(n) ne sont pas tous dans cette zone.
Il y a des termes de la suite (sin(n)) qui sont supérieurs à L+1/4 et d'autres qui sont inférieurs à L-1/4, (par exemple, dans le schéma, sin(8), sin(11) ne sont pas dans la zone rouge ) d'où contradiction.

C'est l'idée, mais il faut voir les toutes situations (qui aboutissent à la même contradiction), suivant la position de la zone rouge par rapport à la bande comprise entre y=-1 et y=+1( où se situe sin(n)).
ça doit faire 5 situations .

Une réflexion personnelle :
J'ignore le degré d'exigence demandé par le professeur, mais je trouve cet énoncé, sans aucune piste de travail, bien difficile en lycée...