Mathématiques :continuité, balayage et convexité
-
MMathouu dernière édition par zipang
Bonjour
Je ne comprends pas mon exercice de maths (pas faute d'avoir essayé)
En voici l'énoncé :Soit ggg la fonction définie sur l'intervalle [1,4][1,4][1,4] par g(x)=x3−1−(1/x)g(x)=x^3-1-(1/x)g(x)=x3−1−(1/x)
- Dresser le tableau de variation de ggg
(j'ai calculé g′(x)g'(x)g′(x) bien entendu et est trouvé 3x2−1/x23x^2-1/x^23x2−1/x2
J'ai trouvé à l'aide ma calculatrice qu'elle était strictement croissante sur l'intervalle [1,4][1,4][1,4] mais elle n'est pas continue en 0. - Etudier le nombre de solutions de l'équation g(x)=10g(x)=10g(x)=10
Je pense qu'il faut utiliser le TVI
J'ai trouvé à la calculatrice une solution, g(998.9)=10g(998.9)=10g(998.9)=10 - Déterminer un encadrement à 10−210^{-2}10−2 près de la solution par balayage à la calculatrice
Je vous remercie d'avance de votre aide et de votre soutien.
*Message ré-écrit avec la notation LaTeXLaTeXLaTeX : référez-vous à nos explications ici : Comment écrire les expressions mathématiques
- Dresser le tableau de variation de ggg
-
Bonjour Mathouu,
Pour la question 1 : Une erreur de signe à la dérivée.
La dérivée de 1x\dfrac{1}{x}x1 est −1x2-\dfrac{1}{x^2}−x21ensuite tu étudies le signe de la dérivée sur le domaine de définition de la fonction
Pour la question 2, c'est bien le TVI qu'il faut utiliser.
-
MMathouu dernière édition par
Merci beaucoup Noemie
-
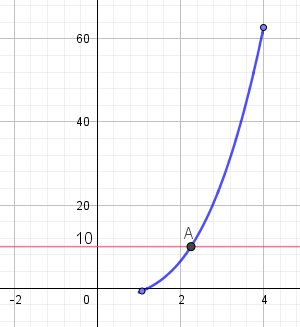
Pour g(x) = 10 la solution appartient à l'intervalle [1 ; 4]
g(998,9)=9,97.108g(998,9) = 9,97 .10^8g(998,9)=9,97.108 !!!g(2,25) = 9,94 et g(2,26) = 10,10
-
mtschoon dernière édition par

Bonjour,
Une illustration pour la 2)