les racines n èmes d'un nombre complexe
-
SsaraSBH dernière édition par mtschoon
bonjour,
on me demande de trouver les racines 6 iémes de z6z^6z6 tel que
z6z^6z6 =-27
arg(z)=pi/6 +2kpi/6 et le module c'est 27
j'ai fait l'argument et le module et puis je me bloque aidez moi svp
-
@
Bonjour sarasSbh,Précise la question et ou est ton problème.
-
mtschoon dernière édition par mtschoon

Bonjour sarasSbh et Noemi,
Je pense avoir compris la question de sarasSbh
sarasSbh, je crois que tu as fait le plus gros , avec la forme exponentielle
Soit z=reiθz=re^{i\theta}z=reiθ
z6=−27z^6=-27z6=−27 <=>r6e6iθ=27eiπr^6e^{6i\theta}=27e^{i\pi}r6e6iθ=27eiπ
Fais attention au module
27 est le module de z6z^6z6. Il faut en déduire le module de zzz
r6=27r^6=27r6=27 <=> r=2716r=27^{\frac{1}{6}}r=2761 <=> r=312r=3^{\frac{1}{2}}r=321 <=>r=3r=\sqrt 3r=3
θ=π6+2kπ6\theta=\frac{\pi}{6}+\frac{2k\pi}{6}θ=6π+62kπ avec k∈Zk\in Zk∈Z
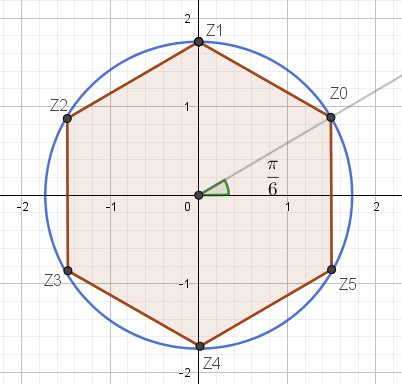
Les 6 racines 6ièmes de -27 sont donc les complexes :
$\displaystyle\fbox{z=\sqrt 3e^{i(\frac{\pi}{6}+\frac{2k\pi}{6})}}$
Reposte si besoin.
-
SsaraSBH dernière édition par
-
mtschoon dernière édition par mtschoon

De rien saraSBH,
Si tu veux les racines carrées de -1-i sous la forme exponentielle, tu peux aller voir dans le topic concerné.
https://forum.mathforu.com/topic/30372/les-racines-carrées-des-nombres-complexes
-
mtschoon dernière édition par mtschoon

Complément : Représentation graphique des six racines 6ièmes de -27, dans le plan complexe