Résolution d'équation selon un paramètre m
-
Lakhlifa Ammari dernière édition par Casebas
étudier selon la valeur du paramétre m les solutions de l equation x^3-3x+m-1=0. c'est une question lie a l etude de la fonction F(x)=x^3-3x
-
Bonjour Lakhlifa-ammari ,
La question est : Etudier le nombre de solutions ou les solutions de l'équation ?
si la question est le nombre de solutions :
Cherche le nombre de points d'intersection de la droite y = 1-m avec la fonction fff.
Exemple si m = 1 y = 0, trois solutions
Si m compris dans l'intervalle ]-1; 3 [, .....
-
@lakhlifa-ammari Un petit bonjour ne fait pas de mal, et permet de demander de l'aide en bonne intelligence avec un peu de respect pour nos gentils modérateurs

-
mtschoon dernière édition par mtschoon

Bonjour tout le monde

Lakhlifa Ammari, j'espère que tu tiendras compte du conseil de Casebas, si tu as besoin de notre aide à l'avenir...
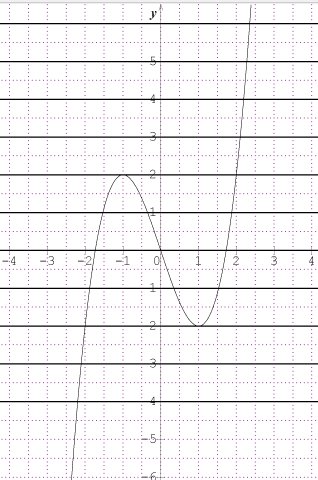
Une illustration graphique de la question :
Les droites d'équation y=1-m sont représentées ici pour m entier compris entre -5 et 5, c'est à dire pour 1-m entier compris entre -4 et 6
-
BBlack-Jack dernière édition par mtschoon
Bonjour,
L'étude des variations de f(x) = x³-3x devrait te permettre de montrer que :
Par l'étude du signe de f'(x) ... en déduire dans quels domaines de x f est croissante ou décroissante.
en déduire que :
f a un minimum local en x = -1 et que ce min vaut f(-1) = 2
f a un maximum local en x = 1 et que ce max vaut f(1) = -2et aussi que lim(x--> -oo) f(x) = -oo et lim(x--> oo) f(x) = oo
Tu peux alors tracer le tableau de variations de f... et le graphe de f(x).
Et en déduire directement les réponses à la question 2.
Si -m+1 < -2, la droite d'équation y = -m+1 coupe la courbe de f(x) en 1 seul point --> 1 solution réelle à x^3-3x+m-1 = 0
Si -m+1 = -2, ...
Si - 2 < -m+1 < 2, ...
Si Si -m+1 = 2, ...(modification effectuée, pour plus de rigueur)
Si Si -m+1 > 2, ...
@Black-Jack
Comme tu l'indiquais, j'ai modifié ton erreur sur l'avant-dernière ligne de ta réponse.
-
Lakhlifa Ammari dernière édition par mtschoon
MERCI INFINIMENT
-
Lakhlifa Ammari dernière édition par
@Casebas OK la prochaine fois je vais dire bonjour ou bonsoir