La dérivée et la valeur absolue

Bonjour à tous j'espère que vous allez bien !
J'ai une question concernant la dérivation
J'ai une fonction f(x)=arctan (x+1)/(x+1)
Je dois prouver que |f'(x)| inférieur ou égal à 1/2 (pour tout x appartient à ]0;1[ )
J'ai calculé la dérivée et j'ai trouvé

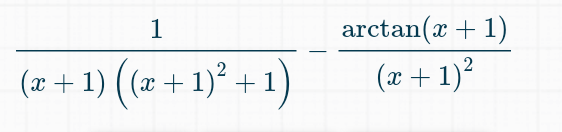
f'(x)<0
Mais je sais pas l'étape suivante
Pouvez-vous m'aider s'il vous plaît !

Bonjour Mathématicienne,

Cherche un majorant sur ]0;1[.

@noemi Merci ! J'ai utilisé une autre manière j'ai simplement calculer |f'(x)|-1/2 ( mais parfois ça ne donne rien; pour trouver le majorant je doit calculer f"(x) n'est ce pas? )

Dans la valeur absolue, tu as une différence, tu cherches le terme le plus grand et tu le majores.
Tu utilises directement la dérivée.
Sur l'intervalle ]0;1[,
comment varie $x+1)^2$ ?
arc tan (x+1) ?

L'écriture de la fonction est-elle correcte ?

Bonjour Mathématicienne et bonjour Noemi,

Je suis perplexe sur cette question...

Mathématicienne, la fonction est-elle vraiment définie par $f(x)=Arctan(x+1)x+1f(x)=\dfrac{Arctan(x+1)}{x+1}$ ?

Si c'est le cas, le domaine de définition et de dérivabilité est R / {-1}
Sur ce domaine, f'(x) est bien la bonne expression (si f(x) est la bonne expression) mais cette dérivée est vraiment "lourde" à manipuler...

Si tu représentes f' sur ta calculette par exemple, tu constateras qu'elle est strictement comprise entre -1/2 et 1/2 ( plus précisément comprise entre -0.29... et +0.29...) pour tout x du domaine donc à forciori |f'| est strictement inférieure à 1/2 ( plus précisément inférieure +0.29...)

Je joins la représentation graphique de |f'| (eu rouge) et de y=1/2 (en bleu)
(Pour -1 (valeur interdite) , le graphique donne 0 qui est le prolongement par continuité.)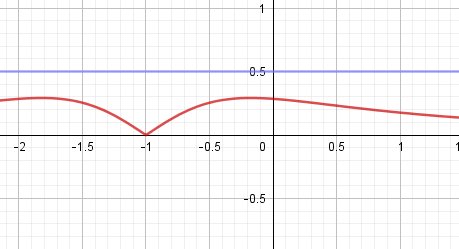

Vouloir prouver que $\le \frac{1}{2}$ sur ]0,1[ ne me semble pas avoir d'intérêt.

J'ai un doute sur l'énoncé donné...
Si besoin, vérifie l'expression de f(x) et donne tout l'énoncé pour qu'on puisse en comprendre la finalité